Jeffrey Dinitz
An analysis of NK and generalized NK landscapes
Feb 14, 2013
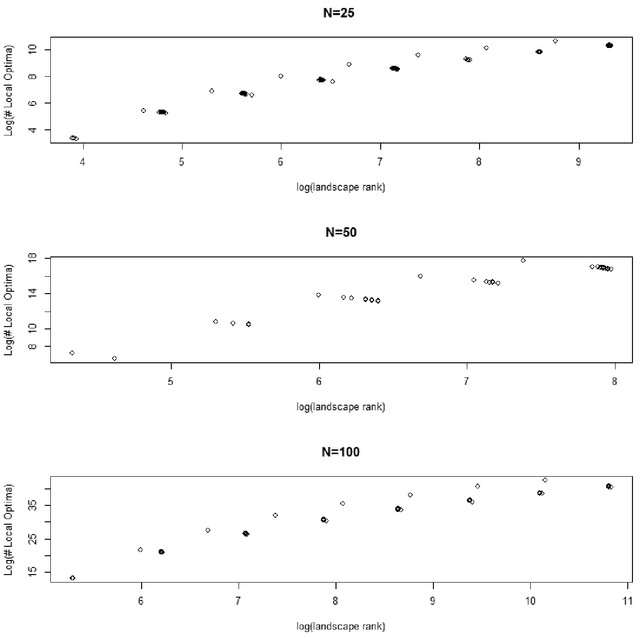
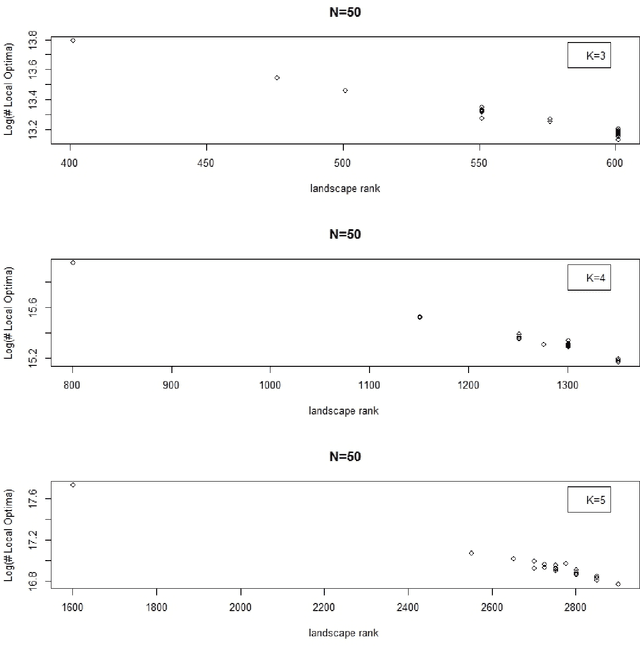
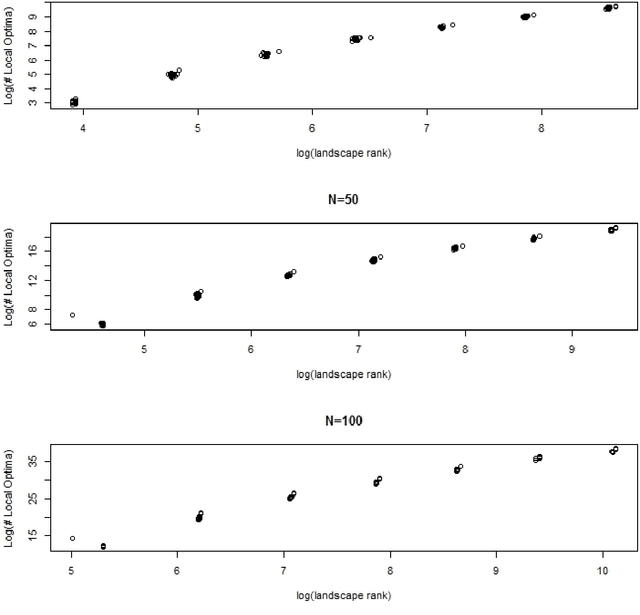
Abstract:Simulated landscapes have been used for decades to evaluate search strategies whose goal is to find the landscape location with maximum fitness. Applications include modeling the capacity of enzymes to catalyze reactions and the clinical effectiveness of medical treatments. Understanding properties of landscapes is important for understanding search difficulty. This paper presents a novel and transparent characterization of NK landscapes. We prove that NK landscapes can be represented by parametric linear interaction models where model coefficients have meaningful interpretations. We derive the statistical properties of the model coefficients, providing insight into how the NK algorithm parses importance to main effects and interactions. An important insight derived from the linear model representation is that the rank of the linear model defined by the NK algorithm is correlated with the number of local optima, a strong determinant of landscape complexity and search difficulty. We show that the maximal rank for an NK landscape is achieved through epistatic interactions that form partially balanced incomplete block designs. Finally, an analytic expression representing the expected number of local optima on the landscape is derived, providing a way to quickly compute the expected number of local optima for very large landscapes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge