Empirical Bayesian image restoration by Langevin sampling with a denoising diffusion implicit prior

Score-based diffusion methods provide a powerful strategy to solve image restoration tasks by flexibly combining a pre-trained foundational prior model with a likelihood function specified during test time. Such methods are predominantly derived from two stochastic processes: reversing Ornstein-Uhlenbeck, which underpins the celebrated denoising diffusion probabilistic models (DDPM) and denoising diffusion implicit models (DDIM), and the Langevin diffusion process. The solutions delivered by DDPM and DDIM are often remarkably realistic, but they are not always consistent with measurements because of likelihood intractability issues and the associated required approximations. Alternatively, using a Langevin process circumvents the intractable likelihood issue, but usually leads to restoration results of inferior quality and longer computing times. This paper presents a novel and highly computationally efficient image restoration method that carefully embeds a foundational DDPM denoiser within an empirical Bayesian Langevin algorithm, which jointly calibrates key model hyper-parameters as it estimates the model's posterior mean. Extensive experimental results on three canonical tasks (image deblurring, super-resolution, and inpainting) demonstrate that the proposed approach improves on state-of-the-art strategies both in image estimation accuracy and computing time.

Bayesian estimation of regularization and PSF parameters for Wiener-Hunt deconvolution

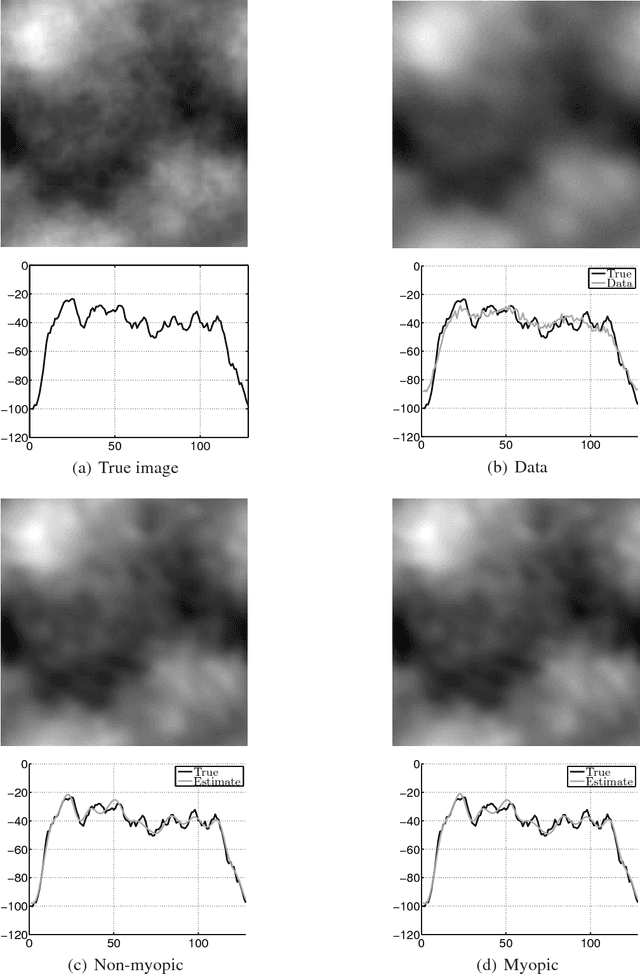
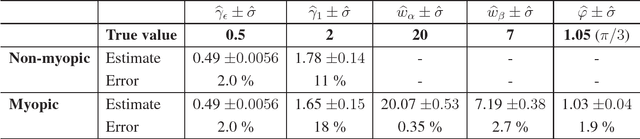
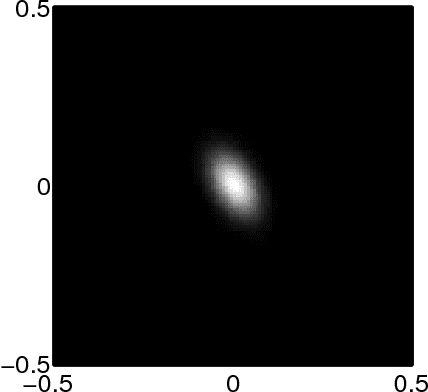
This paper tackles the problem of image deconvolution with joint estimation of PSF parameters and hyperparameters. Within a Bayesian framework, the solution is inferred via a global a posteriori law for unknown parameters and object. The estimate is chosen as the posterior mean, numerically calculated by means of a Monte-Carlo Markov chain algorithm. The estimates are efficiently computed in the Fourier domain and the effectiveness of the method is shown on simulated examples. Results show precise estimates for PSF parameters and hyperparameters as well as precise image estimates including restoration of high-frequencies and spatial details, within a global and coherent approach.