SupEuclid: Extremely Simple, High Quality OoD Detection with Supervised Contrastive Learning and Euclidean Distance

Out-of-Distribution (OoD) detection has developed substantially in the past few years, with available methods approaching, and in a few cases achieving, perfect data separation on standard benchmarks. These results generally involve large or complex models, pretraining, exposure to OoD examples or extra hyperparameter tuning. Remarkably, it is possible to achieve results that can exceed many of these state-of-the-art methods with a very simple method. We demonstrate that ResNet18 trained with Supervised Contrastive Learning (SCL) produces state-of-the-art results out-of-the-box on near and far OoD detection benchmarks using only Euclidean distance as a scoring rule. This may obviate the need in some cases for more sophisticated methods or larger models, and at the very least provides a very strong, easy to use baseline for further experimentation and analysis.

Simple High Quality OoD Detection with L2 Normalization

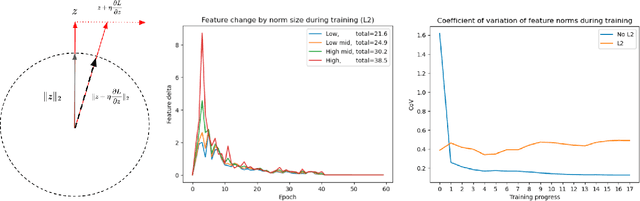
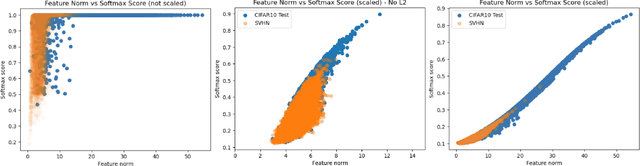
We propose a simple modification to standard ResNet architectures during training--L2 normalization over feature space--that produces results competitive with state-of-the-art Out-of-Distribution (OoD) detection performance. When L2 normalization is removed at test time, the L2 norm of feature vectors becomes a surprisingly good proxy for network uncertainty, whereas this behaviour is not nearly as effective when training without L2 normalization. Intuitively, familiar images result in large magnitude vectors, while unfamiliar images result in small magnitudes. Notably, this is achievable with almost no additional cost during training, and no cost at test time.

Inducing Early Neural Collapse in Deep Neural Networks for Improved Out-of-Distribution Detection

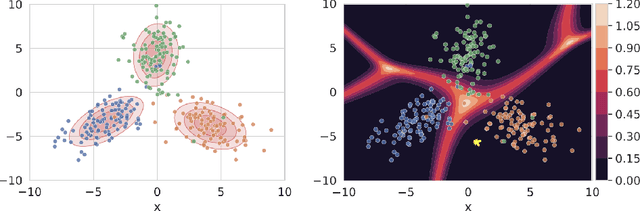
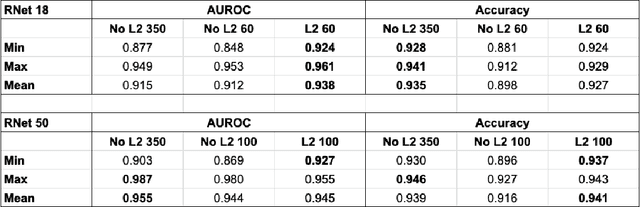
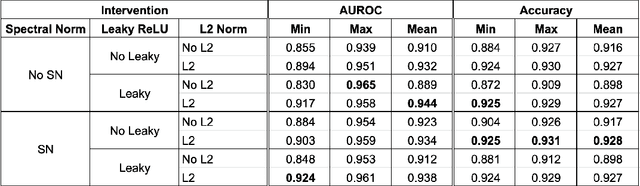
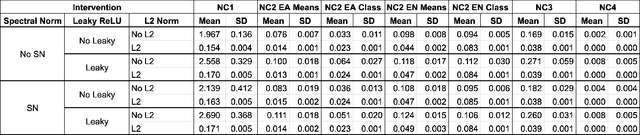
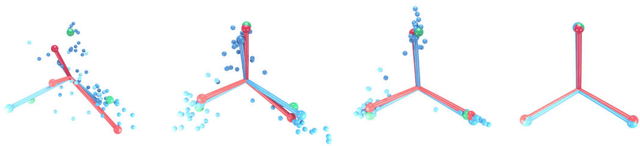
We propose a simple modification to standard ResNet architectures--L2 regularization over feature space--that substantially improves out-of-distribution (OoD) performance on the previously proposed Deep Deterministic Uncertainty (DDU) benchmark. This change also induces early Neural Collapse (NC), which we show is an effect under which better OoD performance is more probable. Our method achieves comparable or superior OoD detection scores and classification accuracy in a small fraction of the training time of the benchmark. Additionally, it substantially improves worst case OoD performance over multiple, randomly initialized models. Though we do not suggest that NC is the sole mechanism or a comprehensive explanation for OoD behaviour in deep neural networks (DNN), we believe NC's simple mathematical and geometric structure can provide a framework for analysis of this complex phenomenon in future work.