Dual JPEG Compatibility: a Reliable and Explainable Tool for Image Forensics

Given a JPEG pipeline (compression or decompression), this paper shows how to find the antecedent of a 8 x 8 block. If it exists, the block is compatible with the pipeline. For unaltered images, all blocks are always compatible with the original pipeline; however, for manipulated images, this is not always the case. This article demonstrates the potential of compatibility concepts for JPEG image forensics. It presents a solution to the main challenge of finding a block antecedent in a high-dimensional space. This solution relies on a local search algorithm with restrictions on the search space. We show that inpainting, copy-move, or splicing applied after a JPEG compression can be turned into three different mismatch problems and be detected. In particular, when the image is re-compressed after the modification, we can detect the manipulation if the quality factor of the second compression is higher than the first one. Our method can pinpoint forgeries down to the JPEG block with great detection power and without False Positive. We compare our method with two state-of-the-art models on localizing inpainted forgeries after a simple or a double compression. We show that under our working assumptions, it outperforms those models for most experiments.

Side-Informed Steganography for JPEG Images by Modeling Decompressed Images

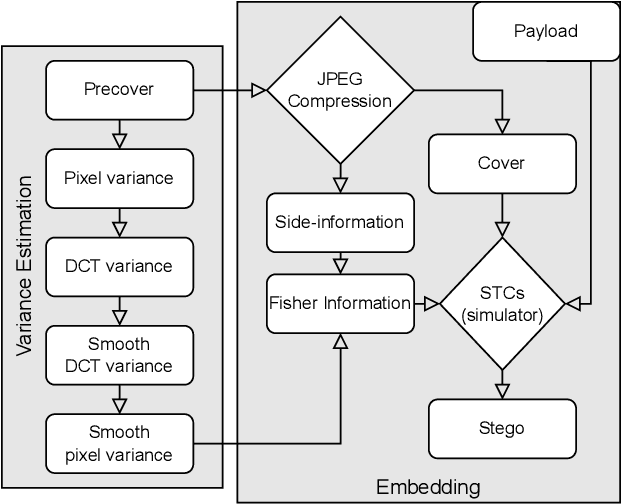
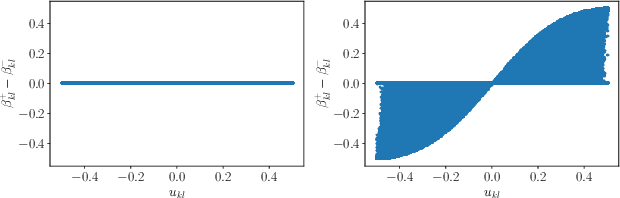
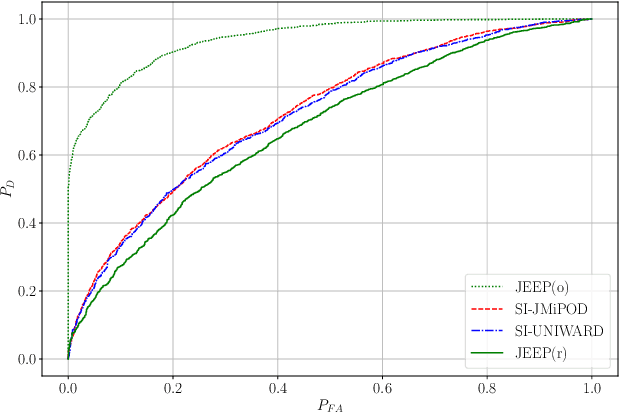
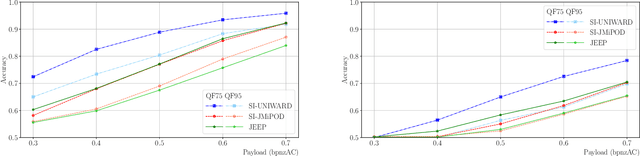
Side-informed steganography has always been among the most secure approaches in the field. However, a majority of existing methods for JPEG images use the side information, here the rounding error, in a heuristic way. For the first time, we show that the usefulness of the rounding error comes from its covariance with the embedding changes. Unfortunately, this covariance between continuous and discrete variables is not analytically available. An estimate of the covariance is proposed, which allows to model steganography as a change in the variance of DCT coefficients. Since steganalysis today is best performed in the spatial domain, we derive a likelihood ratio test to preserve a model of a decompressed JPEG image. The proposed method then bounds the power of this test by minimizing the Kullback-Leibler divergence between the cover and stego distributions. We experimentally demonstrate in two popular datasets that it achieves state-of-the-art performance against deep learning detectors. Moreover, by considering a different pixel variance estimator for images compressed with Quality Factor 100, even greater improvements are obtained.

Errorless Robust JPEG Steganography using Outputs of JPEG Coders

Robust steganography is a technique of hiding secret messages in images so that the message can be recovered after additional image processing. One of the most popular processing operations is JPEG recompression. Unfortunately, most of today's steganographic methods addressing this issue only provide a probabilistic guarantee of recovering the secret and are consequently not errorless. That is unacceptable since even a single unexpected change can make the whole message unreadable if it is encrypted. We propose to create a robust set of DCT coefficients by inspecting their behavior during recompression, which requires access to the targeted JPEG compressor. This is done by dividing the DCT coefficients into 64 non-overlapping lattices because one embedding change can potentially affect many other coefficients from the same DCT block during recompression. The robustness is then combined with standard steganographic costs creating a lattice embedding scheme robust against JPEG recompression. Through experiments, we show that the size of the robust set and the scheme's security depends on the ordering of lattices during embedding. We verify the validity of the proposed method with three typical JPEG compressors and benchmark its security for various embedding payloads, three different ways of ordering the lattices, and a range of Quality Factors. Finally, this method is errorless by construction, meaning the embedded message will always be readable.