Improved Regret Bounds for Tracking Experts with Memory

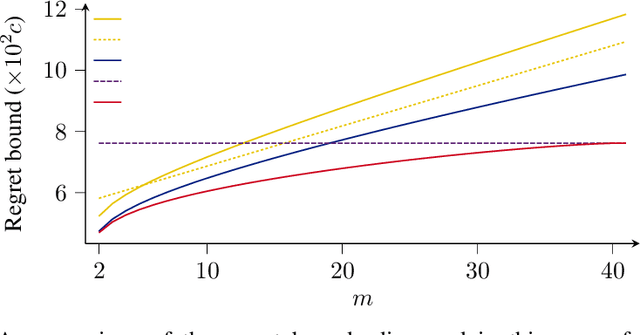
We address the problem of sequential prediction with expert advice in a non-stationary environment with long-term memory guarantees in the sense of Bousquet and Warmuth [4]. We give a linear-time algorithm that improves on the best known regret bounds [26]. This algorithm incorporates a relative entropy projection step. This projection is advantageous over previous weight-sharing approaches in that weight updates may come with implicit costs as in for example portfolio optimization. We give an algorithm to compute this projection step in linear time, which may be of independent interest.

Predicting Switching Graph Labelings with Cluster Specialists

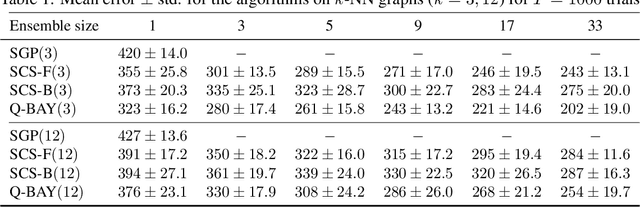
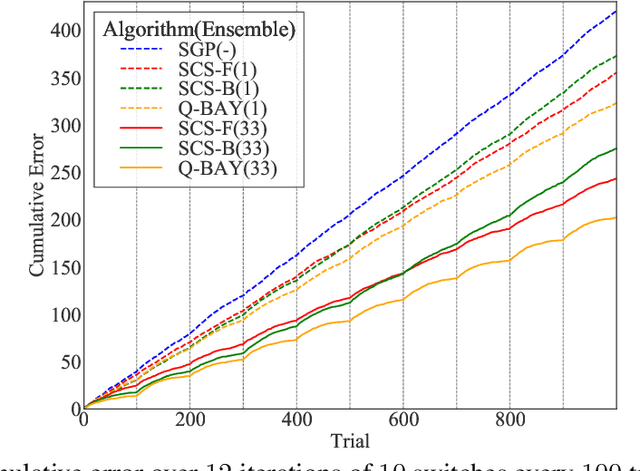
We address the problem of predicting the labeling of a graph in an online setting when the labeling is changing over time. We provide three mistake-bounded algorithms based on three paradigmatic methods for online algorithm design. The algorithm with the strongest guarantee is a quasi-Bayesian classifier which requires $\mathcal{O}(t \log n)$ time to predict at trial $t$ on an $n$-vertex graph. The fastest algorithm (with the weakest guarantee) is based on a specialist [10] approach and surprisingly only requires $\mathcal{O}(\log n)$ time on any trial $t$. We also give an algorithm based on a kernelized Perceptron with an intermediate per-trial time complexity of $\mathcal{O}(n)$ and a mistake bound which is not strictly comparable. Finally, we provide experiments on simulated data comparing these methods.