Predicting Switching Graph Labelings with Cluster Specialists
Paper and Code
Jun 17, 2018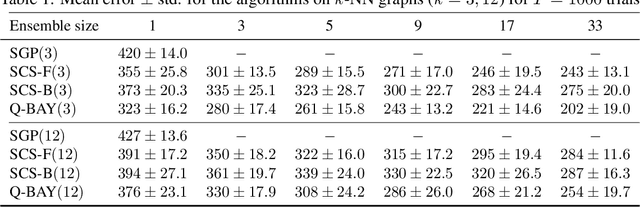
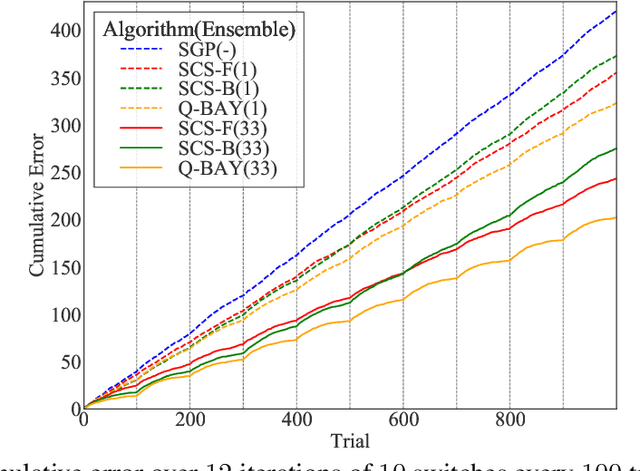
We address the problem of predicting the labeling of a graph in an online setting when the labeling is changing over time. We provide three mistake-bounded algorithms based on three paradigmatic methods for online algorithm design. The algorithm with the strongest guarantee is a quasi-Bayesian classifier which requires $\mathcal{O}(t \log n)$ time to predict at trial $t$ on an $n$-vertex graph. The fastest algorithm (with the weakest guarantee) is based on a specialist [10] approach and surprisingly only requires $\mathcal{O}(\log n)$ time on any trial $t$. We also give an algorithm based on a kernelized Perceptron with an intermediate per-trial time complexity of $\mathcal{O}(n)$ and a mistake bound which is not strictly comparable. Finally, we provide experiments on simulated data comparing these methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge