Practical Calculation of Gittins Indices for Multi-armed Bandits

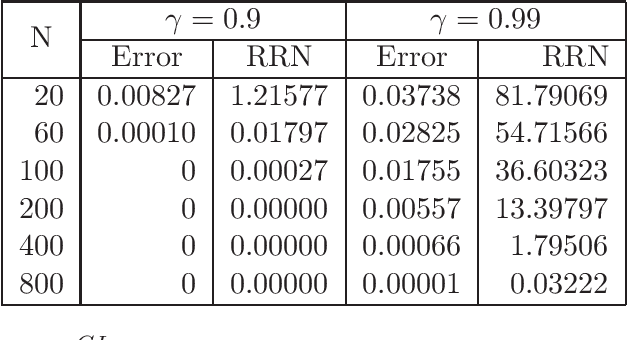
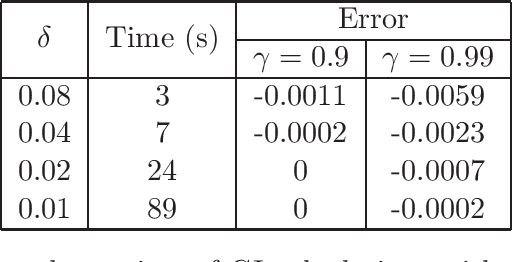
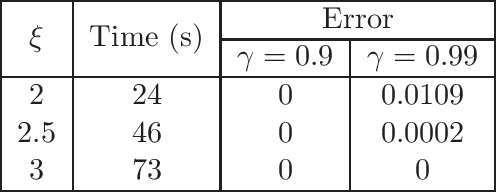
Gittins indices provide an optimal solution to the classical multi-armed bandit problem. An obstacle to their use has been the common perception that their computation is very difficult. This paper demonstrates an accessible general methodology for the calculating Gittins indices for the multi-armed bandit with a detailed study on the cases of Bernoulli and Gaussian rewards. With accompanying easy-to-use open source software, this work removes computation as a barrier to using Gittins indices in these commonly found settings.

On the Identification and Mitigation of Weaknesses in the Knowledge Gradient Policy for Multi-Armed Bandits

The Knowledge Gradient (KG) policy was originally proposed for online ranking and selection problems but has recently been adapted for use in online decision making in general and multi-armed bandit problems (MABs) in particular. We study its use in a class of exponential family MABs and identify weaknesses, including a propensity to take actions which are dominated with respect to both exploitation and exploration. We propose variants of KG which avoid such errors. These new policies include an index heuristic which deploys a KG approach to develop an approximation to the Gittins index. A numerical study shows this policy to perform well over a range of MABs including those for which index policies are not optimal. While KG does not make dominated actions when bandits are Gaussian, it fails to be index consistent and appears not to enjoy a performance advantage over competitor policies when arms are correlated to compensate for its greater computational demands.