Performance Comparison of Surrogate-Assisted Evolutionary Algorithms on Computational Fluid Dynamics Problems

Surrogate-assisted evolutionary algorithms (SAEAs) are recently among the most widely studied methods for their capability to solve expensive real-world optimization problems. However, the development of new methods and benchmarking with other techniques still relies almost exclusively on artificially created problems. In this paper, we use two real-world computational fluid dynamics problems to compare the performance of eleven state-of-the-art single-objective SAEAs. We analyze the performance by investigating the quality and robustness of the obtained solutions and the convergence properties of the selected methods. Our findings suggest that the more recently published methods, as well as the techniques that utilize differential evolution as one of their optimization mechanisms, perform significantly better than the other considered methods.

Computational and Exploratory Landscape Analysis of the GKLS Generator

The GKLS generator is one of the most used testbeds for benchmarking global optimization algorithms. In this paper, we conduct both a computational analysis and the Exploratory Landscape Analysis (ELA) of the GKLS generator. We utilize both canonically used and newly generated classes of GKLS-generated problems and show their use in benchmarking three state-of-the-art methods (from evolutionary and deterministic communities) in dimensions 5 and 10. We show that the GKLS generator produces ``needle in a haystack'' type problems that become extremely difficult to optimize in higher dimensions. Furthermore, we conduct the ELA on the GKLS generator and then compare it to the ELA of two other widely used benchmark sets (BBOB and CEC 2014), and discuss the meaningfulness of the results.

The Evolutionary Computation Methods No One Should Use

The center-bias (or zero-bias) operator has recently been identified as one of the problems plaguing the benchmarking of evolutionary computation methods. This operator lets the methods that utilize it easily optimize functions that have their respective optima in the center of the feasible set. In this paper, we describe a simple procedure that can be used to identify methods that incorporate a center-bias operator and use it to investigate 90 evolutionary computation methods that were published between 1987 and 2022. We show that more than half (47 out of the 90) of the considered methods have the center-bias problem. We also show that the center-bias is a relatively new phenomenon (with the first identified method being from 2012), but its inclusion has become extremely prevalent in the last few years. Lastly, we briefly discuss the possible root causes of this issue.

Are metaheuristics worth it? A computational comparison between nature-inspired and deterministic techniques on black-box optimization problems

In the field of derivative-free optimization, both of its main branches, the deterministic and nature-inspired techniques, experienced in recent years substantial advancement. In this paper, we provide an extensive computational comparison of selected methods from each of these branches. The chosen representatives were either standard and well-utilized methods, or the best-performing methods from recent numerical comparisons. The computational comparison was performed on five different benchmark sets and the results were analyzed in terms of performance, time complexity, and convergence properties of the selected methods. The results showed that, when dealing with situations where the objective function evaluations are relatively cheap, the nature-inspired methods have a significantly better performance than their deterministic counterparts. However, in situations when the function evaluations are costly or otherwise prohibited, the deterministic methods might provide more consistent and overall better results.

Lipschitz-based Surrogate Model for High-dimensional Computationally Expensive Problems

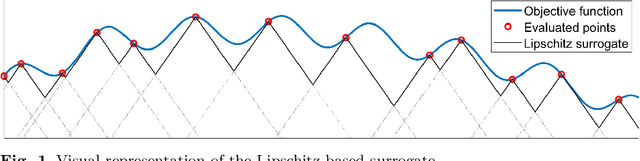
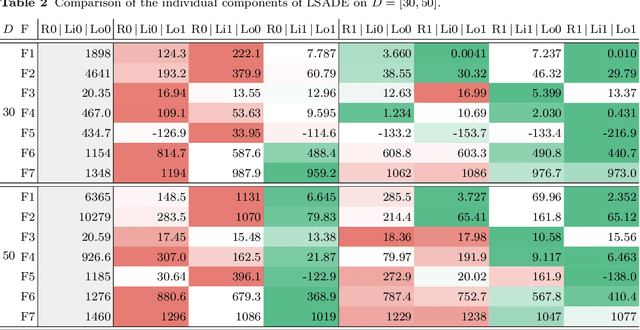
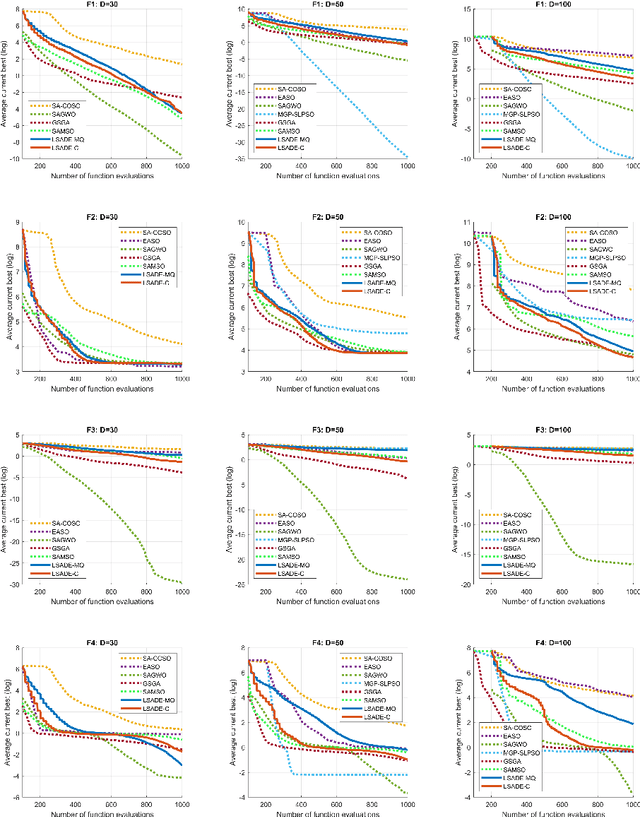
Standard evolutionary optimization algorithms assume that the evaluation of the objective and constraint functions is straightforward and computationally cheap. However, in many real-world optimization problems, the computations of the objective function or constraints involve computationally expensive numerical simulations or physical experiments. Surrogate-assisted evolutionary algorithms (SAEAs) have recently gained increased attention because of their search capabilities for solving these computationally expensive optimization problems. The main idea of SAEAs is the integration of an evolutionary algorithm with a selected surrogate model. In this paper, we propose a novel surrogate model based on a Lipschitz underestimation of the expensive-to-compute objective function. We also develop a differential evolution-based algorithm, that utilizes the Lipschitz-based surrogate model, along with a standard radial basis function surrogate model and a local search procedure. This algorithm, called Lipschitz Surrogate-assisted Differential Evolution (LSADE), is designed for high-dimensional computationally expensive problems. The experimental results on seven benchmark functions of dimensions 30, 50, 100, and 200 show that the proposed method utilizing the Lipschitz-based surrogate model is competitive compared with the state-of-the-art algorithms under a limited computational budget, being especially effective for the very complicated benchmark functions in high dimensions.