Lipschitz-based Surrogate Model for High-dimensional Computationally Expensive Problems

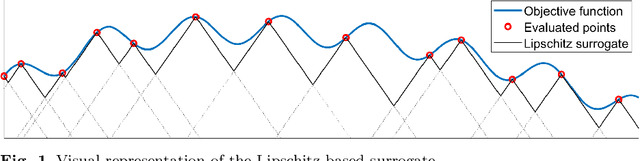
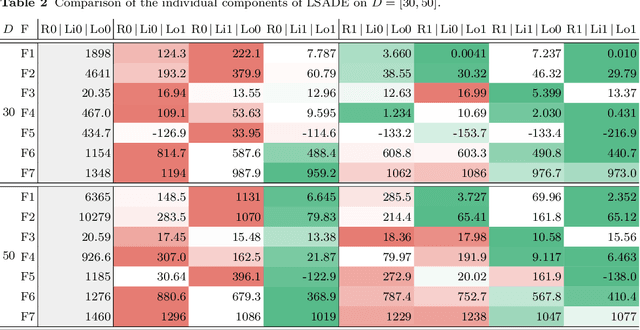
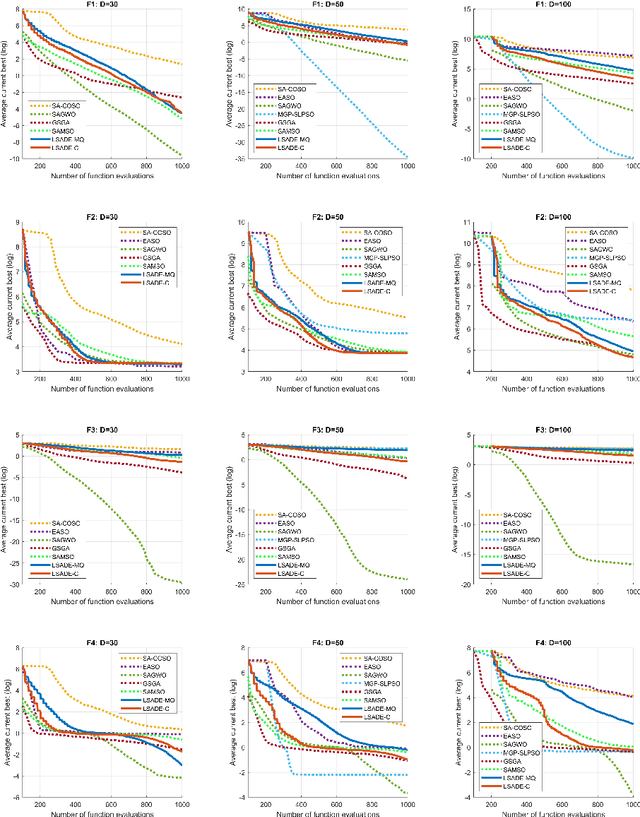
Standard evolutionary optimization algorithms assume that the evaluation of the objective and constraint functions is straightforward and computationally cheap. However, in many real-world optimization problems, the computations of the objective function or constraints involve computationally expensive numerical simulations or physical experiments. Surrogate-assisted evolutionary algorithms (SAEAs) have recently gained increased attention because of their search capabilities for solving these computationally expensive optimization problems. The main idea of SAEAs is the integration of an evolutionary algorithm with a selected surrogate model. In this paper, we propose a novel surrogate model based on a Lipschitz underestimation of the expensive-to-compute objective function. We also develop a differential evolution-based algorithm, that utilizes the Lipschitz-based surrogate model, along with a standard radial basis function surrogate model and a local search procedure. This algorithm, called Lipschitz Surrogate-assisted Differential Evolution (LSADE), is designed for high-dimensional computationally expensive problems. The experimental results on seven benchmark functions of dimensions 30, 50, 100, and 200 show that the proposed method utilizing the Lipschitz-based surrogate model is competitive compared with the state-of-the-art algorithms under a limited computational budget, being especially effective for the very complicated benchmark functions in high dimensions.