Jaiyam Sharma
Improving Similarity Search with High-dimensional Locality-sensitive Hashing
Dec 05, 2018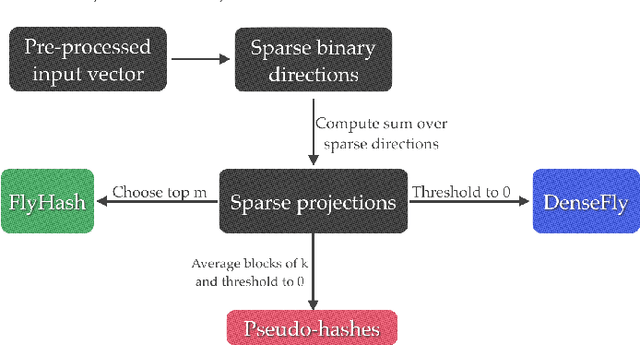
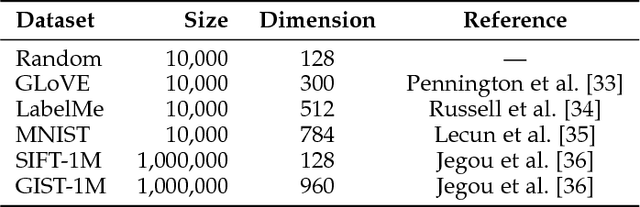
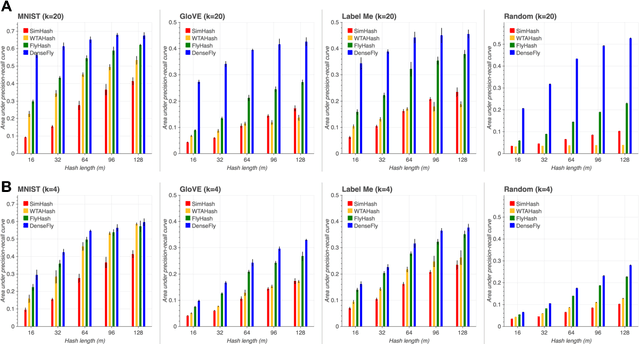
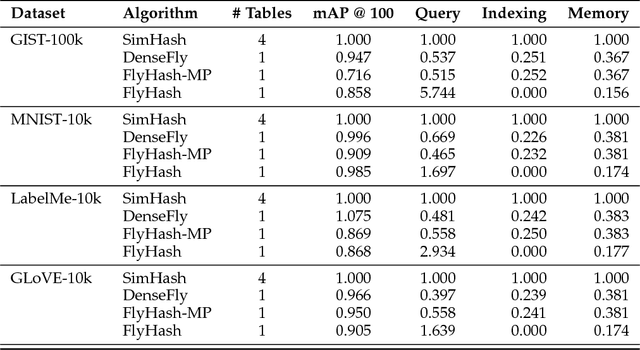
Abstract:We propose a new class of data-independent locality-sensitive hashing (LSH) algorithms based on the fruit fly olfactory circuit. The fundamental difference of this approach is that, instead of assigning hashes as dense points in a low dimensional space, hashes are assigned in a high dimensional space, which enhances their separability. We show theoretically and empirically that this new family of hash functions is locality-sensitive and preserves rank similarity for inputs in any `p space. We then analyze different variations on this strategy and show empirically that they outperform existing LSH methods for nearest-neighbors search on six benchmark datasets. Finally, we propose a multi-probe version of our algorithm that achieves higher performance for the same query time, or conversely, that maintains performance of prior approaches while taking significantly less indexing time and memory. Overall, our approach leverages the advantages of separability provided by high-dimensional spaces, while still remaining computationally efficient
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge