Jaimit Parikh
Integration of AI and mechanistic modeling in generative adversarial networks for stochastic inverse problems
Sep 17, 2020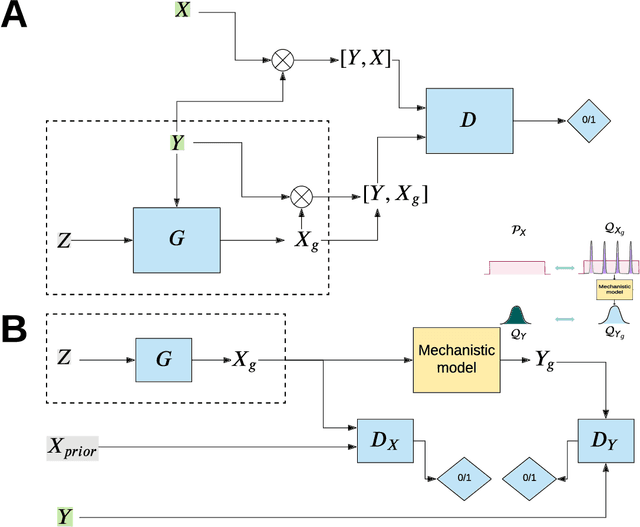
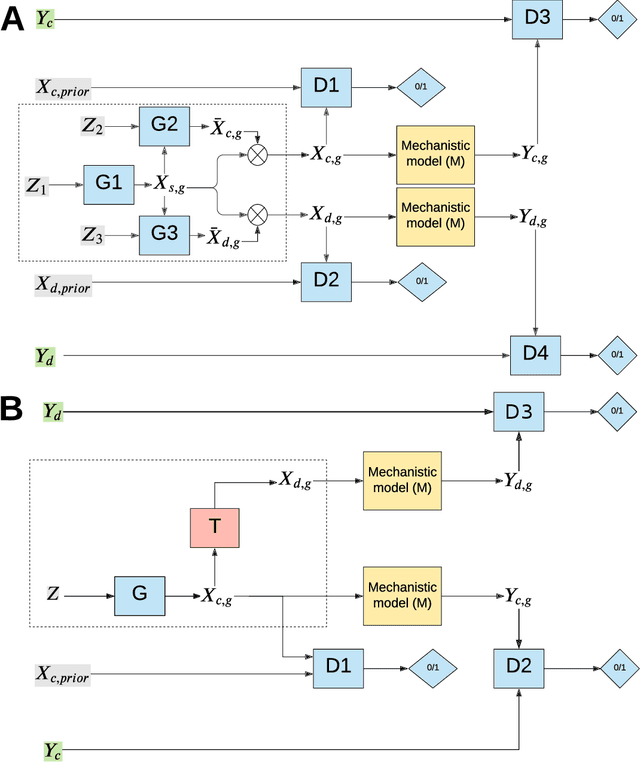
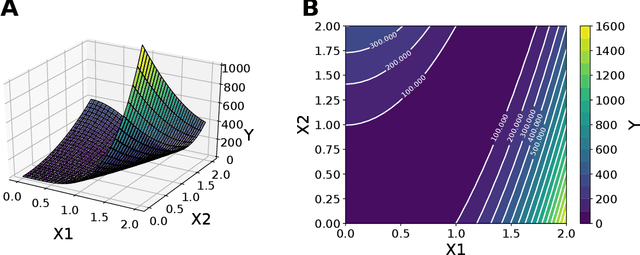
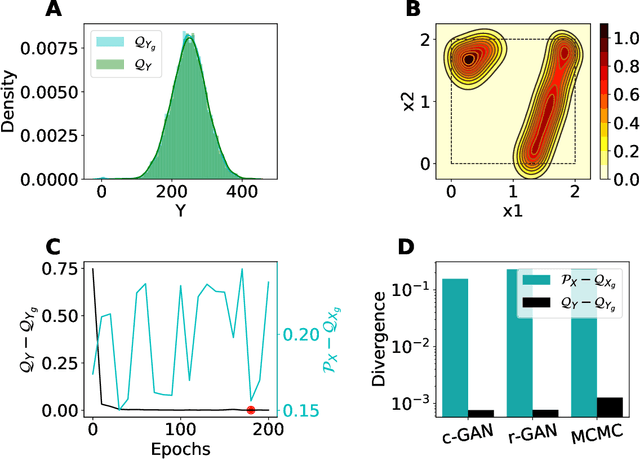
Abstract:The problem of finding distributions of input parameters for deterministic mechanistic models to match distributions of model outputs to stochastic observations, i.e., the "Stochastic Inverse Problem" (SIP), encompasses a range of common tasks across a variety of scientific disciplines. Here, we demonstrate that SIP could be reformulated as a constrained optimization problem and adapted for applications in intervention studies to simultaneously infer model input parameters for two sets of observations, under control conditions and under an intervention. In the constrained optimization problem, the solution of SIP is enforced to accommodate the prior knowledge on the model input parameters and to produce outputs consistent with given observations by minimizing the divergence between the inferred distribution of input parameters and the prior. Unlike in standard SIP, the prior incorporates not only knowledge about model input parameters for objects in each set, but also information on the joint distribution or the deterministic map between the model input parameters in two sets of observations. To solve standard and intervention SIP, we employed conditional generative adversarial networks (GANs) and designed novel GANs that incorporate multiple generators and discriminators and have structures that reflect the underlying constrained optimization problems. This reformulation allows us to build computationally scalable solutions to tackle complex model input parameter inference scenarios, which appear routinely in physics, biophysics, economics and other areas, and which currently could not be handled with existing methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge