E-detectors: a nonparametric framework for online changepoint detection

Sequential changepoint detection is a classical problem with a variety of applications. However, the majority of prior work has been parametric, for example, focusing on exponential families. We develop a fundamentally new and general framework for changepoint detection when the pre- and post-change distributions are nonparametrically specified (and thus composite). Our procedures come with clean, nonasymptotic bounds on the average run length (frequency of false alarms). In certain nonparametric cases (like sub-Gaussian or sub-exponential), we also provide near-optimal bounds on the detection delay following a changepoint. The primary technical tool that we introduce is called an e-detector, which is composed of sums of e-processes -- a fundamental generalization of nonnegative supermartingales -- that are started at consecutive times. We first introduce simple Shiryaev-Roberts and CUSUM-style e-detectors, and then show how to design their mixtures in order to achieve both statistical and computational efficiency. We demonstrate their efficacy in detecting changes in the mean of a bounded random variable without any i.i.d. assumptions, with an application to tracking the performance of a sports team over multiple seasons.

On conditional versus marginal bias in multi-armed bandits

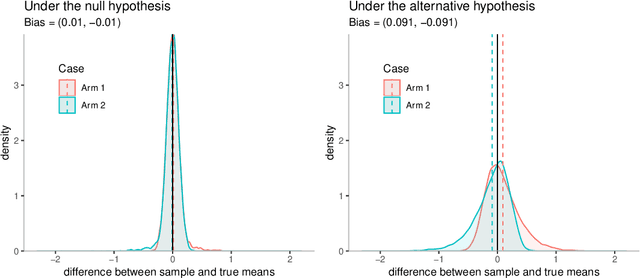
The bias of the sample means of the arms in multi-armed bandits is an important issue in adaptive data analysis that has recently received considerable attention in the literature. Existing results relate in precise ways the sign and magnitude of the bias to various sources of data adaptivity, but do not apply to the conditional inference setting in which the sample means are computed only if some specific conditions are satisfied. In this paper, we characterize the sign of the conditional bias of monotone functions of the rewards, including the sample mean. Our results hold for arbitrary conditioning events and leverage natural monotonicity properties of the data collection policy. We further demonstrate, through several examples from sequential testing and best arm identification, that the sign of the conditional and unconditional bias of the sample mean of an arm can be different, depending on the conditioning event. Our analysis offers new and interesting perspectives on the subtleties of assessing the bias in data adaptive settings.

The bias of the sample mean in multi-armed bandits can be positive or negative

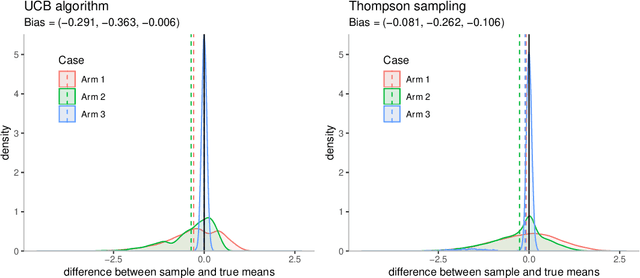
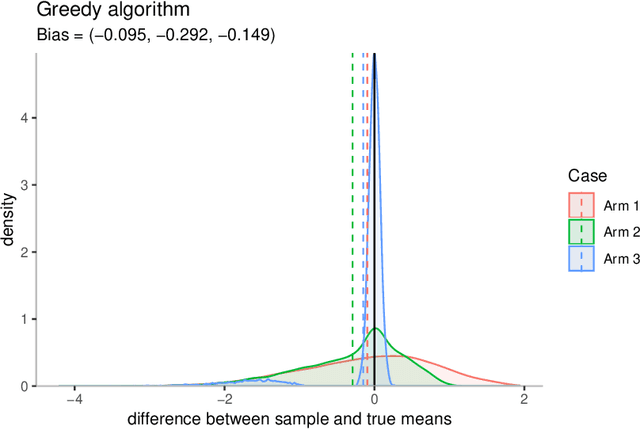
It is well known that in stochastic multi-armed bandits (MAB), the sample mean of an arm is typically not an unbiased estimator of its true mean. In this paper, we decouple three different sources of this selection bias: adaptive \emph{sampling} of arms, adaptive \emph{stopping} of the experiment and adaptively \emph{choosing} which arm to study. Through a new notion called ``optimism'' that captures certain natural monotonic behaviors of algorithms, we provide a clean and unified analysis of how optimistic rules affect the sign of the bias. The main takeaway message is that optimistic sampling induces a negative bias, but optimistic stopping and optimistic choosing both induce a positive bias. These results are derived in a general stochastic MAB setup that is entirely agnostic to the final aim of the experiment (regret minimization or best-arm identification or anything else). We provide examples of optimistic rules of each type, demonstrate that simulations confirm our theoretical predictions, and pose some natural but hard open problems.

On the bias, risk and consistency of sample means in multi-armed bandits

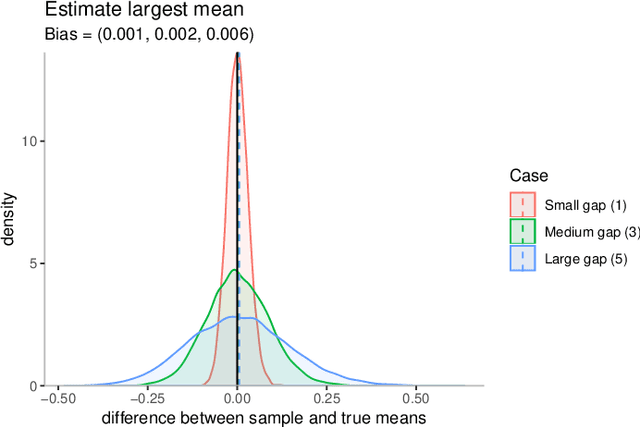
In the classic stochastic multi-armed bandit problem, it is well known that the sample mean for a chosen arm is a biased estimator of its true mean. In this paper, we characterize the effect of four sources of this selection bias: adaptively \emph{sampling} an arm at each step, adaptively \emph{stopping} the data collection, adaptively \emph{choosing} which arm to target for mean estimation, and adaptively \emph{rewinding} the clock to focus on the sample mean of the chosen arm at some past time. We qualitatively characterize data collecting strategies for which the bias induced by adaptive sampling and stopping can be negative or positive. For general parametric and nonparametric classes of distributions with varying tail decays, we provide bounds on the risk (expected Bregman divergence between the sample and true mean) that hold for arbitrary rules for sampling, stopping, choosing and rewinding. These risk bounds are minimax optimal up to log factors, and imply tight bounds on the selection bias and sufficient conditions for their consistency.