On Regularization via Early Stopping for Least Squares Regression

A fundamental problem in machine learning is understanding the effect of early stopping on the parameters obtained and the generalization capabilities of the model. Even for linear models, the effect is not fully understood for arbitrary learning rates and data. In this paper, we analyze the dynamics of discrete full batch gradient descent for linear regression. With minimal assumptions, we characterize the trajectory of the parameters and the expected excess risk. Using this characterization, we show that when training with a learning rate schedule $\eta_k$, and a finite time horizon $T$, the early stopped solution $\beta_T$ is equivalent to the minimum norm solution for a generalized ridge regularized problem. We also prove that early stopping is beneficial for generic data with arbitrary spectrum and for a wide variety of learning rate schedules. We provide an estimate for the optimal stopping time and empirically demonstrate the accuracy of our estimate.

Discrete error dynamics of mini-batch gradient descent for least squares regression

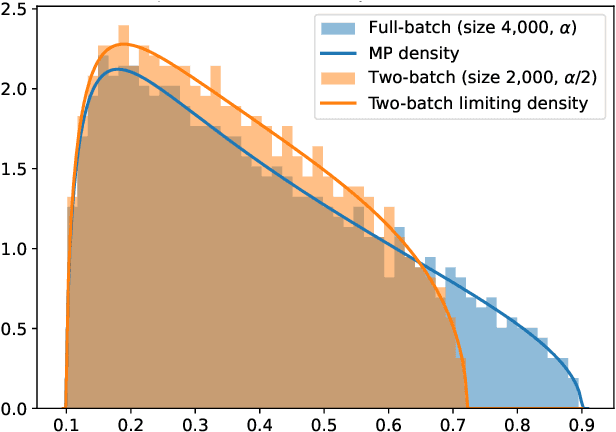
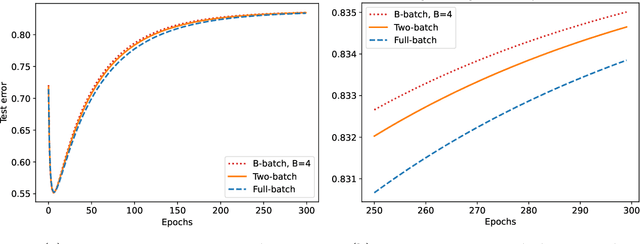
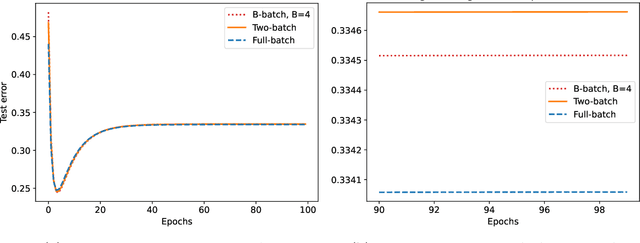
We study the discrete dynamics of mini-batch gradient descent for least squares regression when sampling without replacement. We show that the dynamics and generalization error of mini-batch gradient descent depends on a sample cross-covariance matrix $Z$ between the original features $X$ and a set of new features $\widetilde{X}$, in which each feature is modified by the mini-batches that appear before it during the learning process in an averaged way. Using this representation, we rigorously establish that the dynamics of mini-batch and full-batch gradient descent agree up to leading order with respect to the step size using the linear scaling rule. We also study discretization effects that a continuous-time gradient flow analysis cannot detect, and show that mini-batch gradient descent converges to a step-size dependent solution, in contrast with full-batch gradient descent. Finally, we investigate the effects of batching, assuming a random matrix model, by using tools from free probability theory to numerically compute the spectrum of $Z$.