Efficient Prior Selection in Gaussian Process Bandits with Thompson Sampling

Gaussian process (GP) bandits provide a powerful framework for solving blackbox optimization of unknown functions. The characteristics of the unknown function depends heavily on the assumed GP prior. Most work in the literature assume that this prior is known but in practice this seldom holds. Instead, practitioners often rely on maximum likelihood estimation to select the hyperparameters of the prior - which lacks theoretical guarantees. In this work, we propose two algorithms for joint prior selection and regret minimization in GP bandits based on GP Thompson sampling (GP-TS): Prior-Elimination GP-TS (PE-GP-TS) and HyperPrior GP-TS (HP-GP-TS). We theoretically analyze the algorithms and establish upper bounds for their respective regret. In addition, we demonstrate the effectiveness of our algorithms compared to the alternatives through experiments with synthetic and real-world data.

Combinatorial Gaussian Process Bandits in Bayesian Settings: Theory and Application for Energy-Efficient Navigation

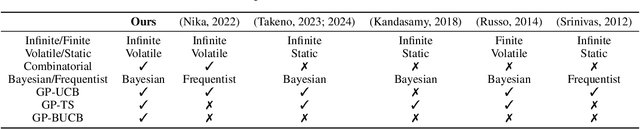
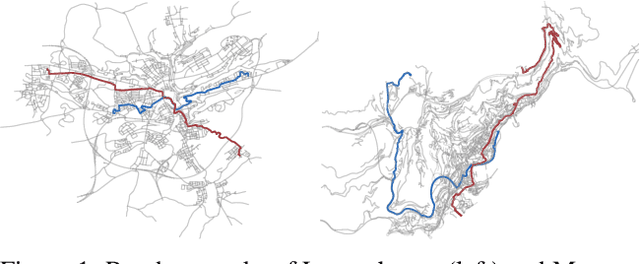
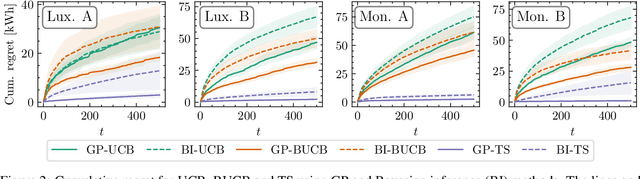
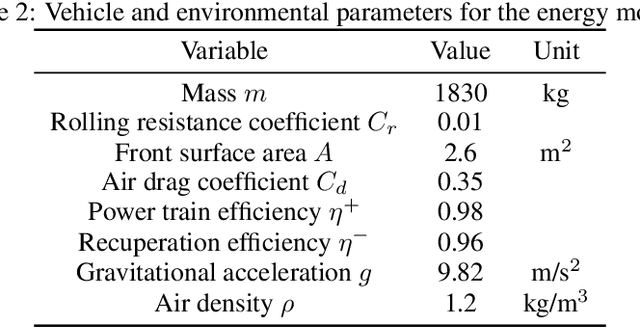
We consider a combinatorial Gaussian process semi-bandit problem with time-varying arm availability. Each round, an agent is provided a set of available base arms and must select a subset of them to maximize the long-term cumulative reward. Assuming the expected rewards are sampled from a Gaussian process (GP) over the arm space, the agent can efficiently learn. We study the Bayesian setting and provide novel Bayesian regret bounds for three GP-based algorithms: GP-UCB, Bayes-GP-UCB and GP-TS. Our bounds extend previous results for GP-UCB and GP-TS to a combinatorial setting with varying arm availability and to the best of our knowledge, we provide the first Bayesian regret bound for Bayes-GP-UCB. Time-varying arm availability encompasses other widely considered bandit problems such as contextual bandits. We formulate the online energy-efficient navigation problem as a combinatorial and contextual bandit and provide a comprehensive experimental study on synthetic and real-world road networks with detailed simulations. The contextual GP model obtains lower regret and is less dependent on the informativeness of the prior compared to the non-contextual Bayesian inference model. In addition, Thompson sampling obtains lower regret than Bayes-UCB for both the contextual and non-contextual model.