Jack Murtagh
Thwarting Adversarial Examples: An $L_0$-RobustSparse Fourier Transform
Dec 12, 2018

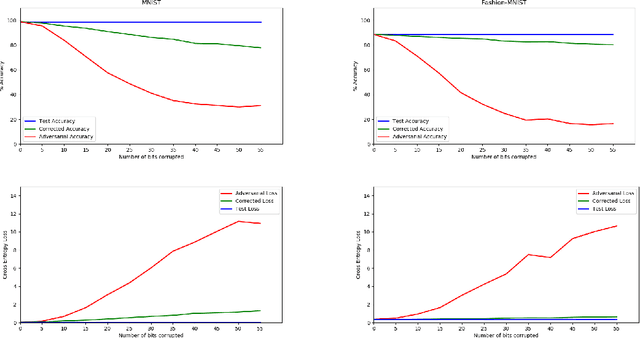

Abstract:We give a new algorithm for approximating the Discrete Fourier transform of an approximately sparse signal that has been corrupted by worst-case $L_0$ noise, namely a bounded number of coordinates of the signal have been corrupted arbitrarily. Our techniques generalize to a wide range of linear transformations that are used in data analysis such as the Discrete Cosine and Sine transforms, the Hadamard transform, and their high-dimensional analogs. We use our algorithm to successfully defend against well known $L_0$ adversaries in the setting of image classification. We give experimental results on the Jacobian-based Saliency Map Attack (JSMA) and the Carlini Wagner (CW) $L_0$ attack on the MNIST and Fashion-MNIST datasets as well as the Adversarial Patch on the ImageNet dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge