Energy-based learning algorithms for analog computing: a comparative study

Energy-based learning algorithms have recently gained a surge of interest due to their compatibility with analog (post-digital) hardware. Existing algorithms include contrastive learning (CL), equilibrium propagation (EP) and coupled learning (CpL), all consisting in contrasting two states, and differing in the type of perturbation used to obtain the second state from the first one. However, these algorithms have never been explicitly compared on equal footing with same models and datasets, making it difficult to assess their scalability and decide which one to select in practice. In this work, we carry out a comparison of seven learning algorithms, namely CL and different variants of EP and CpL depending on the signs of the perturbations. Specifically, using these learning algorithms, we train deep convolutional Hopfield networks (DCHNs) on five vision tasks (MNIST, F-MNIST, SVHN, CIFAR-10 and CIFAR-100). We find that, while all algorithms yield comparable performance on MNIST, important differences in performance arise as the difficulty of the task increases. Our key findings reveal that negative perturbations are better than positive ones, and highlight the centered variant of EP (which uses two perturbations of opposite sign) as the best-performing algorithm. We also endorse these findings with theoretical arguments. Additionally, we establish new SOTA results with DCHNs on all five datasets, both in performance and speed. In particular, our DCHN simulations are 13.5 times faster with respect to Laborieux et al. (2021), which we achieve thanks to the use of a novel energy minimisation algorithm based on asynchronous updates, combined with reduced precision (16 bits).

A Gradient Estimator for Time-Varying Electrical Networks with Non-Linear Dissipation

We propose a method for extending the technique of equilibrium propagation for estimating gradients in fixed-point neural networks to the more general setting of directed, time-varying neural networks by modeling them as electrical circuits. We use electrical circuit theory to construct a Lagrangian capable of describing deep, directed neural networks modeled using nonlinear capacitors and inductors, linear resistors and sources, and a special class of nonlinear dissipative elements called fractional memristors. We then derive an estimator for the gradient of the physical parameters of the network, such as synapse conductances, with respect to an arbitrary loss function. This estimator is entirely local, in that it only depends on information locally available to each synapse. We conclude by suggesting methods for extending these results to networks of biologically plausible neurons, e.g. Hodgkin-Huxley neurons.

Training End-to-End Analog Neural Networks with Equilibrium Propagation

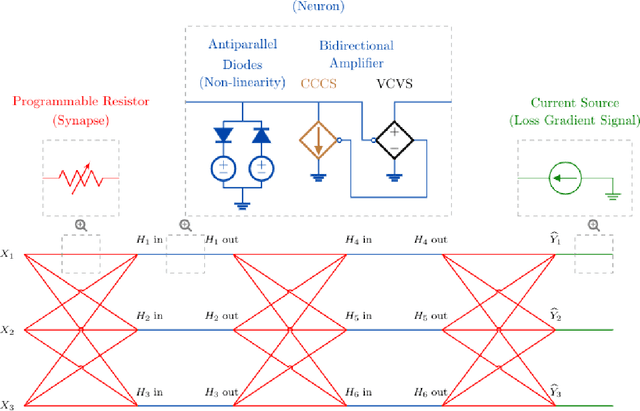
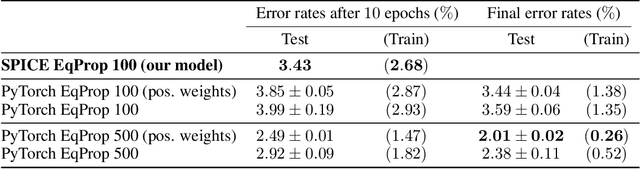
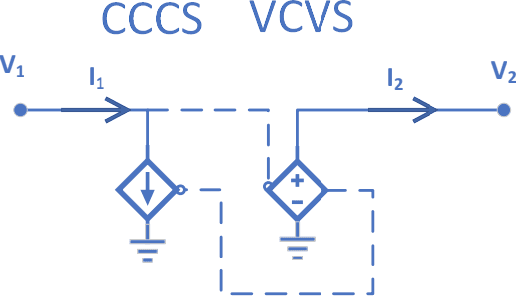
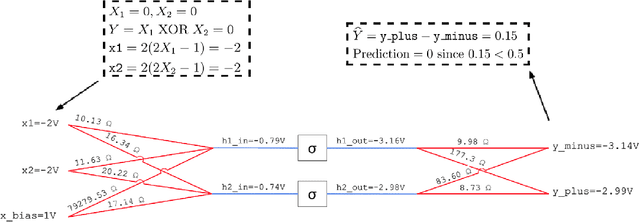
We introduce a principled method to train end-to-end analog neural networks by stochastic gradient descent. In these analog neural networks, the weights to be adjusted are implemented by the conductances of programmable resistive devices such as memristors [Chua, 1971], and the nonlinear transfer functions (or `activation functions') are implemented by nonlinear components such as diodes. We show mathematically that a class of analog neural networks (called nonlinear resistive networks) are energy-based models: they possess an energy function as a consequence of Kirchhoff's laws governing electrical circuits. This property enables us to train them using the Equilibrium Propagation framework [Scellier and Bengio, 2017]. Our update rule for each conductance, which is local and relies solely on the voltage drop across the corresponding resistor, is shown to compute the gradient of the loss function. Our numerical simulations, which use the SPICE-based Spectre simulation framework to simulate the dynamics of electrical circuits, demonstrate training on the MNIST classification task, performing comparably or better than equivalent-size software-based neural networks. Our work can guide the development of a new generation of ultra-fast, compact and low-power neural networks supporting on-chip learning.