Get our free extension to see links to code for papers anywhere online!Free add-on: code for papers everywhere!Free add-on: See code for papers anywhere!
JCS Kadupitiya
Deep Learning Based Integrators for Solving Newton's Equations with Large Timesteps
May 17, 2020Figures and Tables: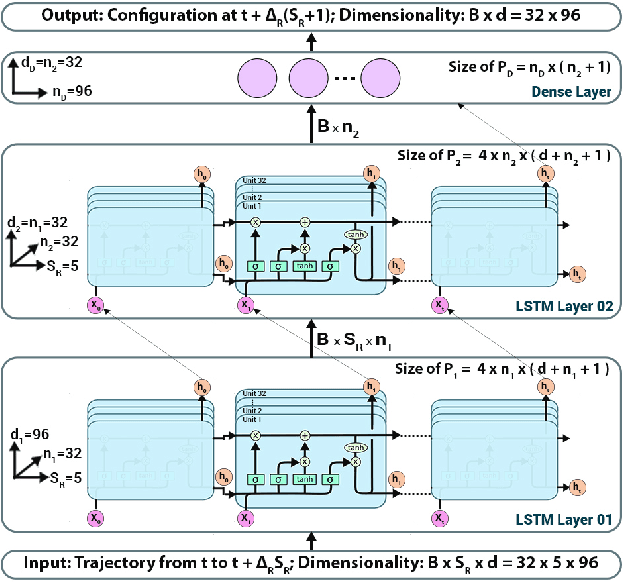

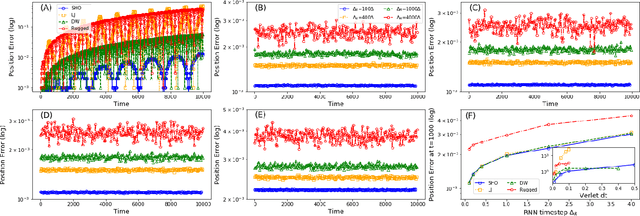
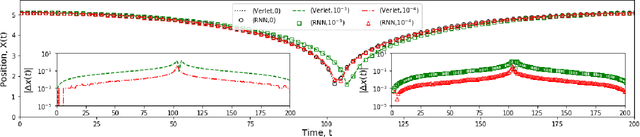




Abstract:Classical molecular dynamics simulations are based on Newton's equations of motion and rely on numerical integrators to solve them. Using a small timestep to avoid discretization errors, Verlet integrators generate a trajectory of particle positions as solutions to Newton's equations. We introduce an integrator based on deep neural networks that is trained on trajectories generated using the Verlet integrator and learns to propagate the dynamics of particles with timestep up to 4000$\times$ larger compared to the Verlet timestep. We demonstrate significant net speedup of up to 32000 for 1 - 16 particle 3D systems and over a variety of force fields.
* 14 pages, 11 figures; content is revised
Via
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge