Regenerativity of Viterbi process for pairwise Markov models

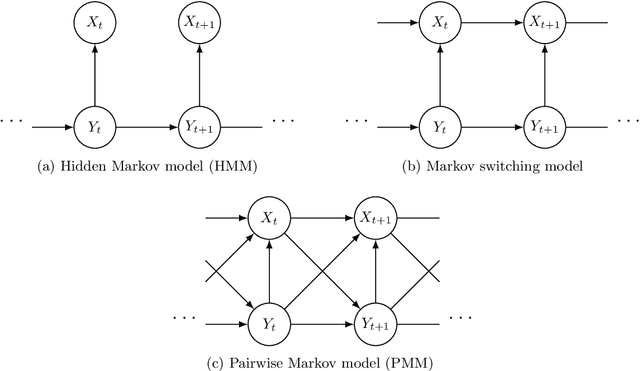
For hidden Markov models one of the most popular estimates of the hidden chain is the Viterbi path -- the path maximising the posterior probability. We consider a more general setting, called the pairwise Markov model (PMM), where the joint process consisting of finite-state hidden process and observation process is assumed to be a Markov chain. It has been recently proven that under some conditions the Viterbi path of the PMM can almost surely be extended to infinity, thereby defining the infinite Viterbi decoding of the observation sequence, called the Viterbi process. This was done by constructing a block of observations, called a barrier, which ensures that the Viterbi path goes trough a given state whenever this block occurs in the observation sequence. In this paper we prove that the joint process consisting of Viterbi process and PMM is regenerative. The proof involves a delicate construction of regeneration times which coincide with the occurrences of barriers. As one possible application of our theory, some results on the asymptotics of the Viterbi training algorithm are derived.

MAP segmentation in Bayesian hidden Markov models: a case study

We consider the problem of estimating the maximum posterior probability (MAP) state sequence for a finite state and finite emission alphabet hidden Markov model (HMM) in the Bayesian setup, where both emission and transition matrices have Dirichlet priors. We study a training set consisting of thousands of protein alignment pairs. The training data is used to set the prior hyperparameters for Bayesian MAP segmentation. Since the Viterbi algorithm is not applicable any more, there is no simple procedure to find the MAP path, and several iterative algorithms are considered and compared. The main goal of the paper is to test the Bayesian setup against the frequentist one, where the parameters of HMM are estimated using the training data.

An evolutionary model that satisfies detailed balance

We propose a class of evolutionary models that involves an arbitrary exchangeable process as the breeding process and different selection schemes. In those models, a new genome is born according to the breeding process, and then a genome is removed according to the selection scheme that involves fitness. Thus the population size remains constant. The process evolves according to a Markov chain, and, unlike in many other existing models, the stationary distribution -- so called mutation-selection equilibrium -- can be easily found and studied. The behaviour of the stationary distribution when the population size increases is our main object of interest. Several phase-transition theorems are proved.

On the accuracy of the Viterbi alignment

In a hidden Markov model, the underlying Markov chain is usually hidden. Often, the maximum likelihood alignment (Viterbi alignment) is used as its estimate. Although having the biggest likelihood, the Viterbi alignment can behave very untypically by passing states that are at most unexpected. To avoid such situations, the Viterbi alignment can be modified by forcing it not to pass these states. In this article, an iterative procedure for improving the Viterbi alignment is proposed and studied. The iterative approach is compared with a simple bunch approach where a number of states with low probability are all replaced at the same time. It can be seen that the iterative way of adjusting the Viterbi alignment is more efficient and it has several advantages over the bunch approach. The same iterative algorithm for improving the Viterbi alignment can be used in the case of peeping, that is when it is possible to reveal hidden states. In addition, lower bounds for classification probabilities of the Viterbi alignment under different conditions on the model parameters are studied.

A generalized risk approach to path inference based on hidden Markov models

Motivated by the unceasing interest in hidden Markov models (HMMs), this paper re-examines hidden path inference in these models, using primarily a risk-based framework. While the most common maximum a posteriori (MAP), or Viterbi, path estimator and the minimum error, or Posterior Decoder (PD), have long been around, other path estimators, or decoders, have been either only hinted at or applied more recently and in dedicated applications generally unfamiliar to the statistical learning community. Over a decade ago, however, a family of algorithmically defined decoders aiming to hybridize the two standard ones was proposed (Brushe et al., 1998). The present paper gives a careful analysis of this hybridization approach, identifies several problems and issues with it and other previously proposed approaches, and proposes practical resolutions of those. Furthermore, simple modifications of the classical criteria for hidden path recognition are shown to lead to a new class of decoders. Dynamic programming algorithms to compute these decoders in the usual forward-backward manner are presented. A particularly interesting subclass of such estimators can be also viewed as hybrids of the MAP and PD estimators. Similar to previously proposed MAP-PD hybrids, the new class is parameterized by a small number of tunable parameters. Unlike their algorithmic predecessors, the new risk-based decoders are more clearly interpretable, and, most importantly, work "out of the box" in practice, which is demonstrated on some real bioinformatics tasks and data. Some further generalizations and applications are discussed in conclusion.

Asymptotic risks of Viterbi segmentation

We consider the maximum likelihood (Viterbi) alignment of a hidden Markov model (HMM). In an HMM, the underlying Markov chain is usually hidden and the Viterbi alignment is often used as the estimate of it. This approach will be referred to as the Viterbi segmentation. The goodness of the Viterbi segmentation can be measured by several risks. In this paper, we prove the existence of asymptotic risks. Being independent of data, the asymptotic risks can be considered as the characteristics of the model that illustrate the long-run behavior of the Viterbi segmentation.