Category theory as a foundation for soft robotics

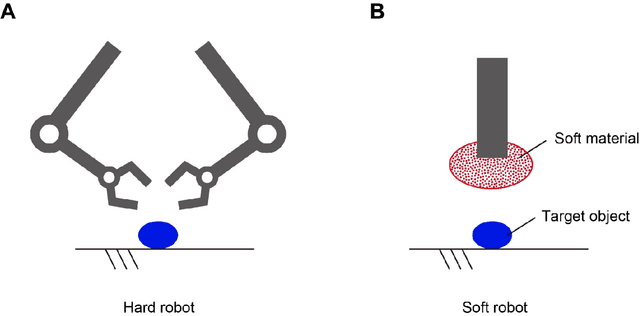
Soft robotics is an emerging field of research where the robot body is composed of compliant and soft materials. It allows the body to bend, twist, and deform to move or to adapt its shape to the environment for grasping, all of which are difficult for traditional hard robots with rigid bodies. However, the theoretical basis and design principles for soft robotics are not well-founded despite their recognized importance. For example, the control of soft robots is outsourced to morphological attributes and natural processes; thus, the coupled relations between a robot and its environment are particularly crucial. In this paper, we propose a mathematical foundation for soft robotics based on category theory, which is a branch of abstract math where any notions can be described by objects and arrows. It allows for a rigorous description of the inherent characteristics of soft robots and their relation to the environment as well as the differences compared to conventional hard robots. We present a notion called the category of mobility that well describes the subject matter. The theory was applied to a model system and analysis to highlight the adaptation behavior observed in universal grippers, which are a typical example of soft robotics. This paper paves the way to developing a theoretical background and design principles for soft robotics.

Local reservoir model for choice-based learning

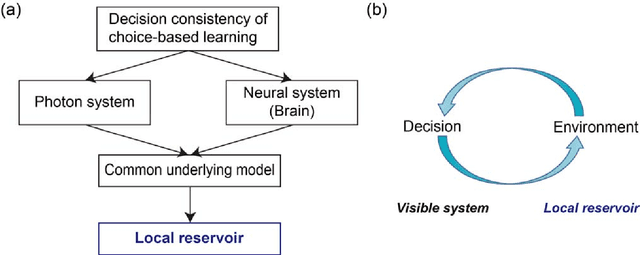
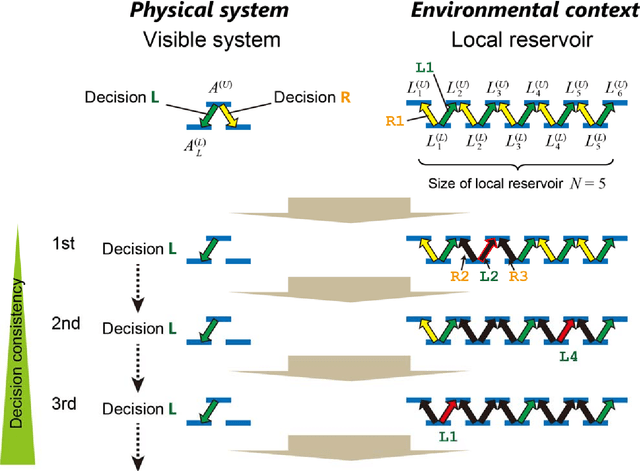
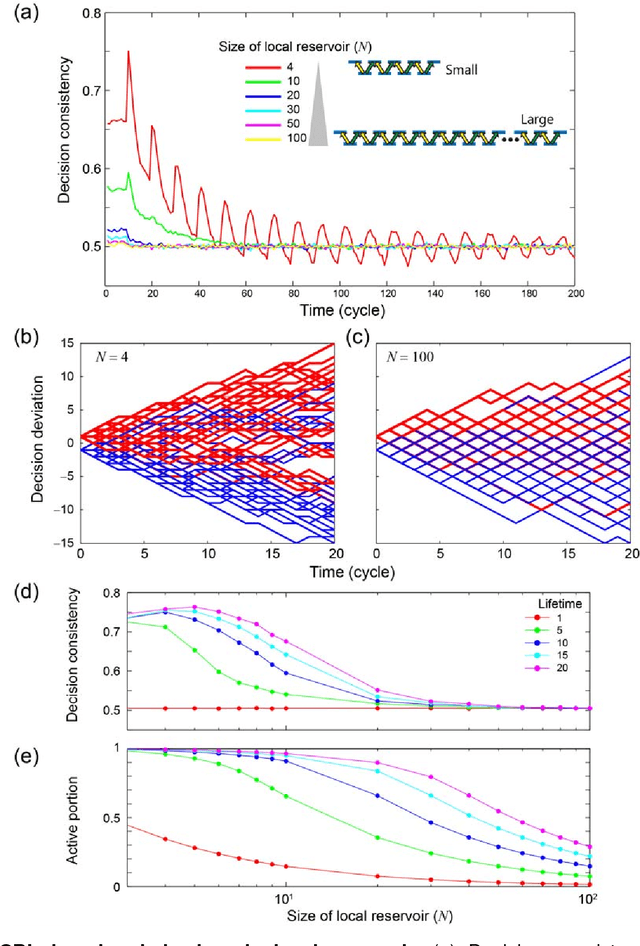
Decision making based on behavioral and neural observations of living systems has been extensively studied in brain science, psychology, and other disciplines. Decision-making mechanisms have also been experimentally implemented in physical processes, such as single photons and chaotic lasers. The findings of these experiments suggest that there is a certain common basis in describing decision making, regardless of its physical realizations. In this study, we propose a local reservoir model to account for choice-based learning (CBL). CBL describes decision consistency as a phenomenon where making a certain decision increases the possibility of making that same decision again later, which has been intensively investigated in neuroscience, psychology, etc. Our proposed model is inspired by the viewpoint that a decision is affected by its local environment, which is referred to as a local reservoir. If the size of the local reservoir is large enough, consecutive decision making will not be affected by previous decisions, thus showing lower degrees of decision consistency in CBL. In contrast, if the size of the local reservoir decreases, a biased distribution occurs within it, which leads to higher degrees of decision consistency in CBL. In this study, an analytical approach on local reservoirs is presented, as well as several numerical demonstrations. Furthermore, a physical architecture for CBL based on single photons is discussed, and the effects of local reservoirs is numerically demonstrated. Decision consistency in human decision-making tasks and in recruiting empirical data are evaluated based on local reservoir. In summary, the proposed local reservoir model paves a path toward establishing a foundation for computational mechanisms and the systematic analysis of decision making on different levels.