Ivan A. Sergienko
Correspondent Banking Networks: Theory and Experiment
Dec 06, 2019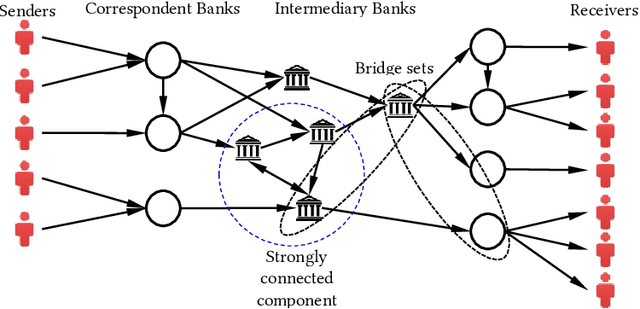
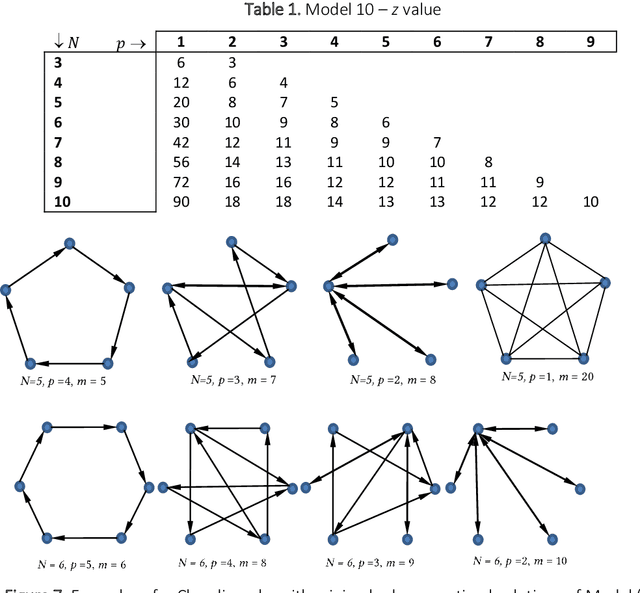


Abstract:We employ the mathematical programming approach in conjunction with the graph theory to study the structure of correspondent banking networks. Optimizing the network requires decisions to be made to onboard, terminate or restrict the bank relationships to optimize the size and overall risk of the network. This study provides theoretical foundation to detect the components, the removal of which does not affect some key properties of the network such as connectivity and diameter. We find that the correspondent banking networks have a feature we call k-accessibility, which helps to drastically reduce the computational burden required for finding the above mentioned components. We prove a number of fundamental theorems related to k-accessible directed graphs, which should be also applicable beyond the particular problem of financial networks. The theoretical findings are verified through the data from a large international bank.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge