Examples of Artificial Perceptions in Optical Character Recognition and Iris Recognition

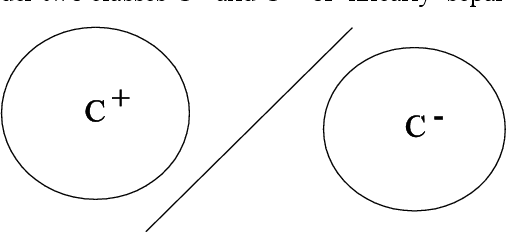
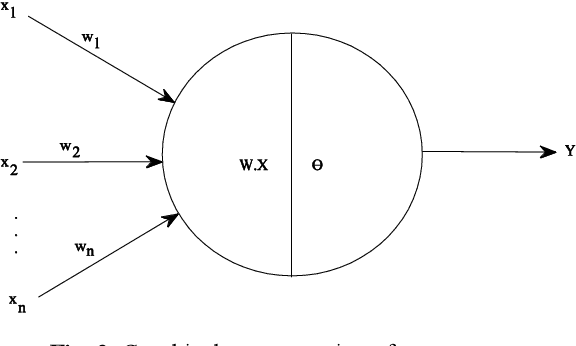
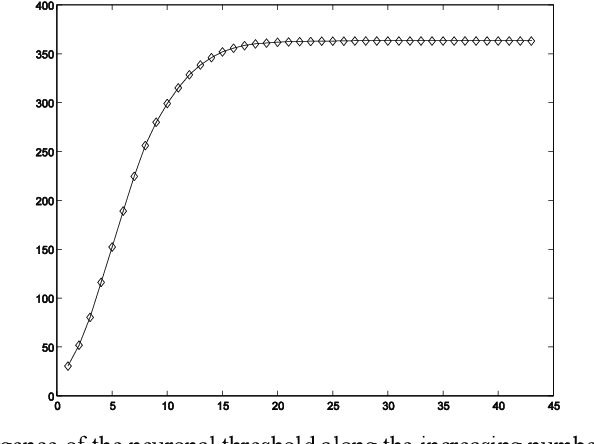
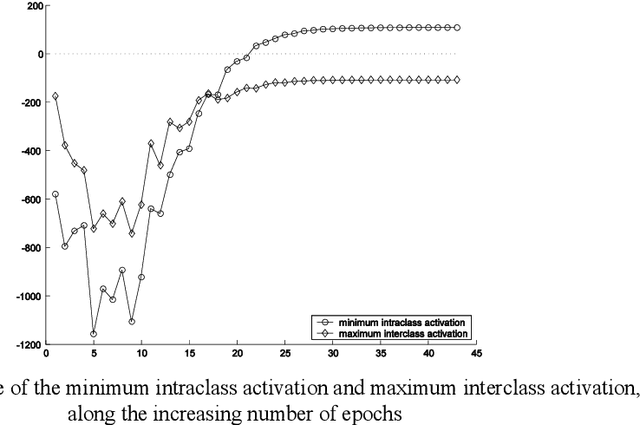
This paper assumes the hypothesis that human learning is perception based, and consequently, the learning process and perceptions should not be represented and investigated independently or modeled in different simulation spaces. In order to keep the analogy between the artificial and human learning, the former is assumed here as being based on the artificial perception. Hence, instead of choosing to apply or develop a Computational Theory of (human) Perceptions, we choose to mirror the human perceptions in a numeric (computational) space as artificial perceptions and to analyze the interdependence between artificial learning and artificial perception in the same numeric space, using one of the simplest tools of Artificial Intelligence and Soft Computing, namely the perceptrons. As practical applications, we choose to work around two examples: Optical Character Recognition and Iris Recognition. In both cases a simple Turing test shows that artificial perceptions of the difference between two characters and between two irides are fuzzy, whereas the corresponding human perceptions are, in fact, crisp.

Noise Influence on the Fuzzy-Linguistic Partitioning of Iris Code Space

This paper analyses the set of iris codes stored or used in an iris recognition system as an f-granular space. The f-granulation is given by identifying in the iris code space the extensions of the fuzzy concepts wolves, goats, lambs and sheep (previously introduced by Doddington as 'animals' of the biometric menagerie) - which together form a partitioning of the iris code space. The main question here is how objective (stable / stationary) this partitioning is when the iris segments are subject to noisy acquisition. In order to prove that the f-granulation of iris code space with respect to the fuzzy concepts that define the biometric menagerie is unstable in noisy conditions (is sensitive to noise), three types of noise (localvar, motion blur, salt and pepper) have been alternatively added to the iris segments extracted from University of Bath Iris Image Database. The results of 180 exhaustive (all-to-all) iris recognition tests are presented and commented here.

The Biometric Menagerie - A Fuzzy and Inconsistent Concept

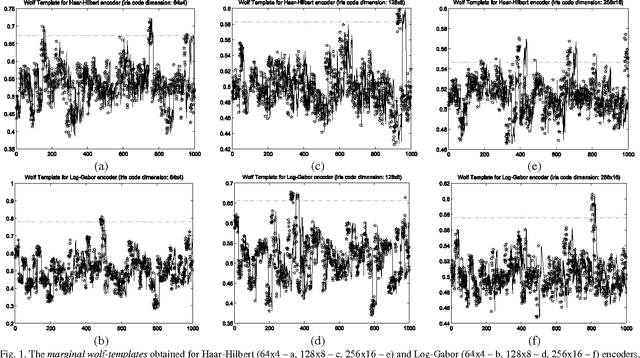
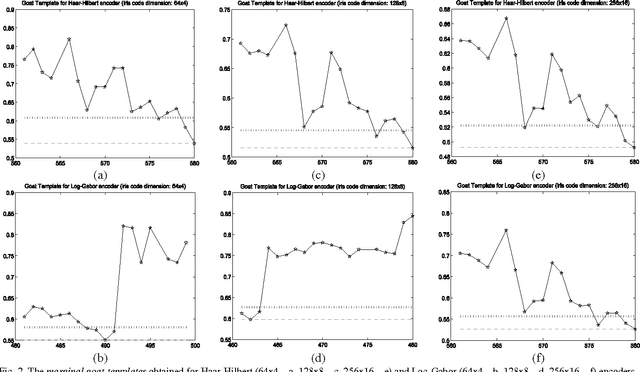
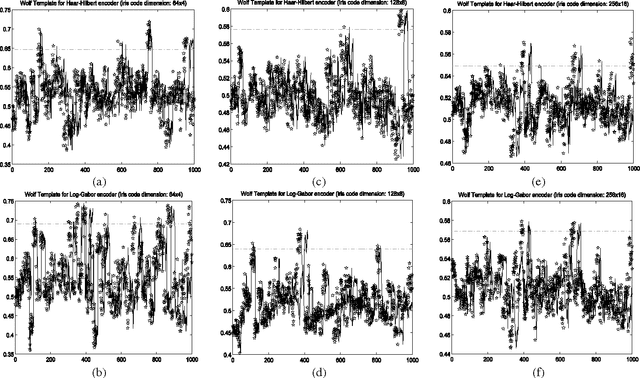
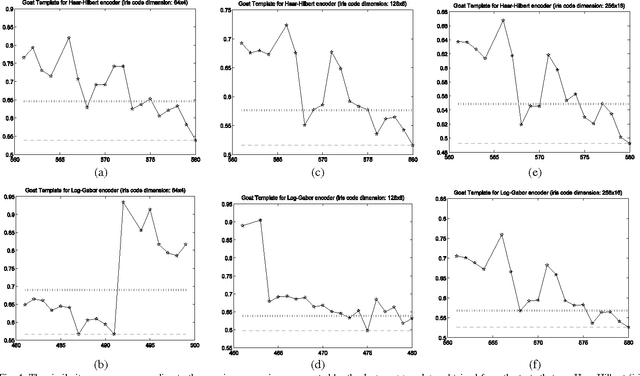
This paper proves that in iris recognition, the concepts of sheep, goats, lambs and wolves - as proposed by Doddington and Yager in the so-called Biometric Menagerie, are at most fuzzy and at least not quite well defined. They depend not only on the users or on their biometric templates, but also on the parameters that calibrate the iris recognition system. This paper shows that, in the case of iris recognition, the extensions of these concepts have very unsharp and unstable (non-stationary) boundaries. The membership of a user to these categories is more often expressed as a degree (as a fuzzy value) rather than as a crisp value. Moreover, they are defined by fuzzy Sugeno rules instead of classical (crisp) definitions. For these reasons, we said that the Biometric Menagerie proposed by Doddington and Yager could be at most a fuzzy concept of biometry, but even this status is conditioned by improving its definition. All of these facts are confirmed experimentally in a series of 12 exhaustive iris recognition tests undertaken for University of Bath Iris Image Database while using three different iris code dimensions (256x16, 128x8 and 64x4), two different iris texture encoders (Log-Gabor and Haar-Hilbert) and two different types of safety models.

Combined Haar-Hilbert and Log-Gabor Based Iris Encoders

This chapter shows that combining Haar-Hilbert and Log-Gabor improves iris recognition performance leading to a less ambiguous biometric decision landscape in which the overlap between the experimental intra- and interclass score distributions diminishes or even vanishes. Haar-Hilbert, Log-Gabor and combined Haar-Hilbert and Log-Gabor encoders are tested here both for single and dual iris approach. The experimental results confirm that the best performance is obtained for the dual iris approach when the iris code is generated using the combined Haar-Hilbert and Log-Gabor encoder, and when the matching score fuses the information from both Haar-Hilbert and Log-Gabor channels of the combined encoder.