Sharpness-Aware Minimization in Genetic Programming

Sharpness-Aware Minimization (SAM) was recently introduced as a regularization procedure for training deep neural networks. It simultaneously minimizes the fitness (or loss) function and the so-called fitness sharpness. The latter serves as a measure of the nonlinear behavior of a solution and does so by finding solutions that lie in neighborhoods having uniformly similar loss values across all fitness cases. In this contribution, we adapt SAM for tree Genetic Programming (TGP) by exploring the semantic neighborhoods of solutions using two simple approaches. By capitalizing upon perturbing input and output of program trees, sharpness can be estimated and used as a second optimization criterion during the evolution. To better understand the impact of this variant of SAM on TGP, we collect numerous indicators of the evolutionary process, including generalization ability, complexity, diversity, and a recently proposed genotype-phenotype mapping to study the amount of redundancy in trees. The experimental results demonstrate that using any of the two proposed SAM adaptations in TGP allows (i) a significant reduction of tree sizes in the population and (ii) a decrease in redundancy of the trees. When assessed on real-world benchmarks, the generalization ability of the elite solutions does not deteriorate.

On The Nature Of The Phenotype In Tree Genetic Programming

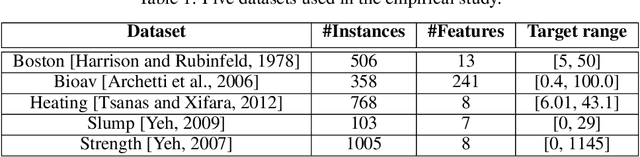
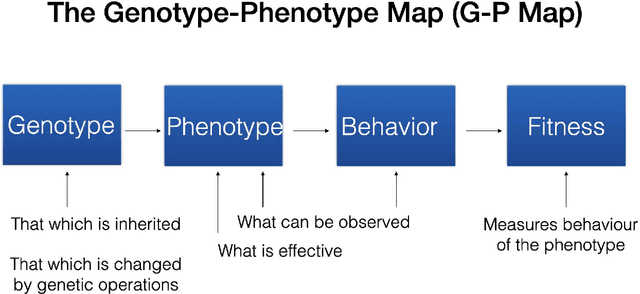
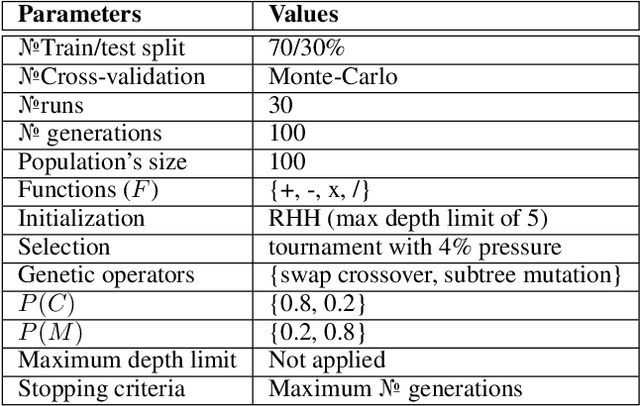
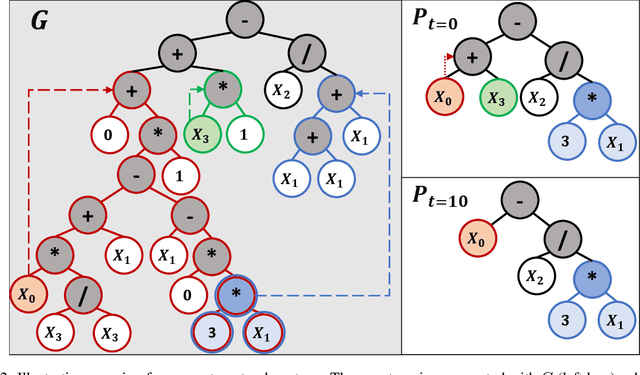
In this contribution, we discuss the basic concepts of genotypes and phenotypes in tree-based GP (TGP), and then analyze their behavior using five benchmark datasets. We show that TGP exhibits the same behavior that we can observe in other GP representations: At the genotypic level trees show frequently unchecked growth with seemingly ineffective code, but on the phenotypic level, much smaller trees can be observed. To generate phenotypes, we provide a unique technique for removing semantically ineffective code from GP trees. The approach extracts considerably simpler phenotypes while not being limited to local operations in the genotype. We generalize this transformation based on a problem-independent parameter that enables a further simplification of the exact phenotype by coarse-graining to produce approximate phenotypes. The concept of these phenotypes (exact and approximate) allows us to clarify what evolved solutions truly predict, making GP models considered at the phenotypic level much better interpretable.