Differential Evolution-Based End-Fire Realized Gain Optimization of Active and Parasitic Arrays

We propose a novel approach for boosting the realized gain in enhanced directivity arrays with both active and parasitic dipoles as radiating elements. The optimization process involves two main objectives: maximizing the end-fire gain and minimizing the reflection coefficient to ensure high realized gain. In the first step, the current excitation vector of the fully driven array is selected to maximize the end-fire gain. Then, all but one of the dipoles are reactively loaded according to their input impedance. Following that, the optimization focuses on the inter-element distance, computing the one that offers a favorable balance between the gain and the total efficiency. This multi-objective optimization leverages the differential evolution (DE) algorithm and utilizes a simple wire dipole as the unit element. Full-wave simulations further confirm the accuracy of our theoretical results. Our two- and three-element parasitic arrays achieve realized gain comparable to state-of-the-art designs, without relying on intricate unit elements or resource-intensive simulations. Moreover, our four- and five-element parasitic arrays deliver the highest realized gain values reported in the literature. The simplicity of our approach is validated by significant time savings, with theoretical models completing optimizations much faster than full-wave simulations. Additionally, a sensitivity analysis confirms the robustness of the proposed optimization algorithm, demonstrating that the optimized design parameters remain effective even under small deviations in loads and element positions. Finally, the proposed parasitic arrays are well-suited for base station antennas due to their compact design, reduced power consumption, and simplified hardware requirements, making them ideal for modern communication systems.

Optimization of Super-Directive Linear Arrays with Differential Evolution for High Realized Gain

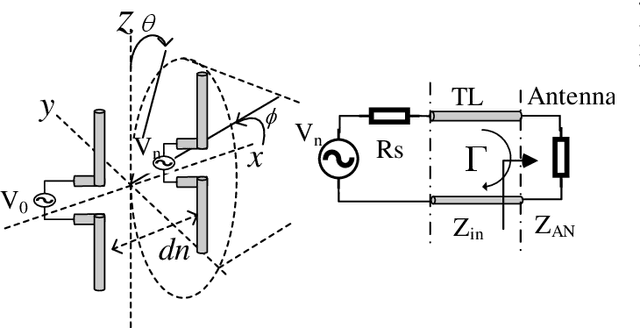
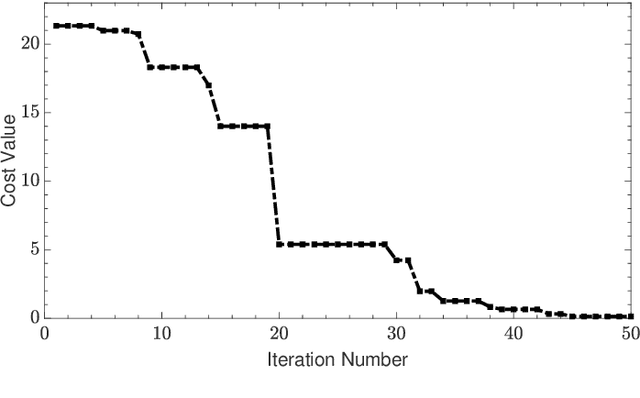
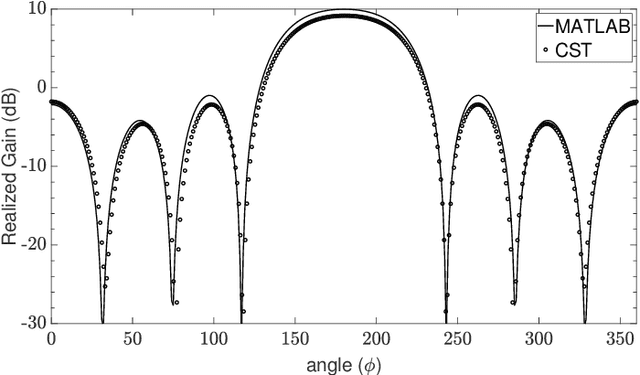
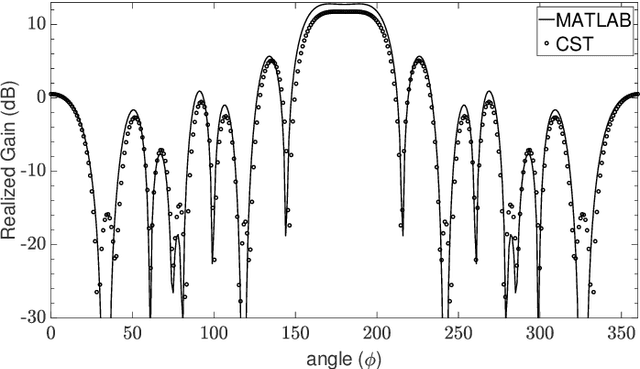
Due to the low impedance and high feeding currents, it is naturally challenging to design super-directive antenna arrays that perfectly match the feed line, and this becomes almost impossible as the number of elements increases. In this paper, we assert that it is crucial to consider the trade-off between directivity and overall efficiency (to achieve high realized gain) before employing super-directive arrays in real-world applications. Given this trade-off (high directivity and low mismatch for high realized gain), a 4-element dipole array (unit array) is optimized using the differential evolution (DE) algorithm. Then, the performance of the unit array in subarray configuration scenarios is analyzed. Finally, the obtained parameters are verified using the CST full-wave simulation software. The results clearly indicate that the proposed unit array is a strong candidate for dense array applications, particularly in the context of massive multiple-input multiple-output (MIMO), thanks to its notable high gain and efficiency.

Super-Directive Antenna Arrays: How Many Elements Do We Need?

Super-directive antenna arrays have faced challenges in achieving high realized gains ever since their introduction in the academic literature. The primary challenges are high impedance mismatches and resistive losses, which become increasingly more dominant as the number of elements increases. Consequently, a critical limitation arises in determining the maximum number of elements that should be utilized to achieve super-directivity, particularly within dense array configurations. This paper addresses precisely this issue through an optimization study to design a super-directive antenna array with a maximum number of elements. An iterative approach is employed to increase the array of elements while sustaining a satisfactory realized gain using the differential evolution (DE) algorithm. Thus, it is observed that super-directivity can be obtained in an array with a maximum of five elements. Our results indicate that the obtained unit array has a $67.20\%$ higher realized gain than a uniform linear array with conventional excitation. For these reasons, these results make the proposed architecture a strong candidate for applications that require densely packed arrays, particularly in the context of massive multiple-input multiple-output (MIMO).