Investigating the Effects of Dynamic Precision Scaling on Neural Network Training

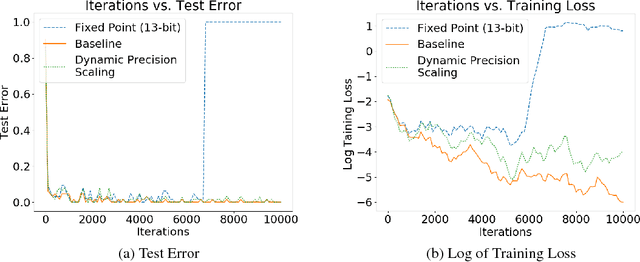
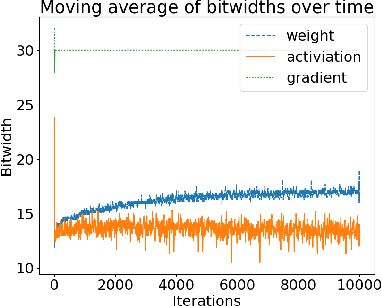
Training neural networks is a time- and compute-intensive operation. This is mainly due to the large amount of floating point tensor operations that are required during training. These constraints limit the scope of design space explorations (in terms of hyperparameter search) for data scientists and researchers. Recent work has explored the possibility of reducing the numerical precision used to represent parameters, activations, and gradients during neural network training as a way to reduce the computational cost of training (and thus reducing training time). In this paper we develop a novel dynamic precision scaling scheme and evaluate its performance, comparing it to previous works. Using stochastic fixed-point rounding, a quantization-error based scaling scheme, and dynamic bit-widths during training, we achieve 98.8% test accuracy on the MNIST dataset using an average bit-width of just 16 bits for weights and 14 bits for activations. This beats the previous state-of-the-art dynamic bit-width precision scaling algorithm.