Learning to Enhance Aperture Phasor Field for Non-Line-of-Sight Imaging

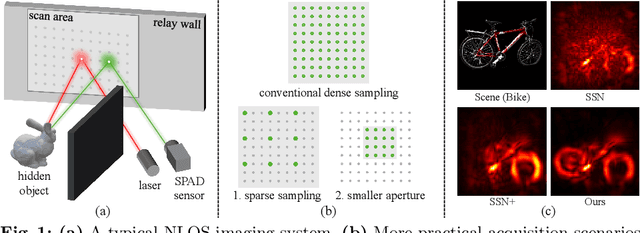
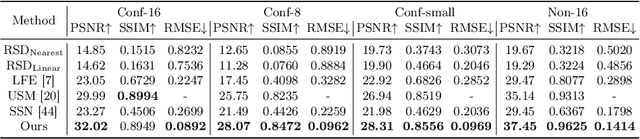
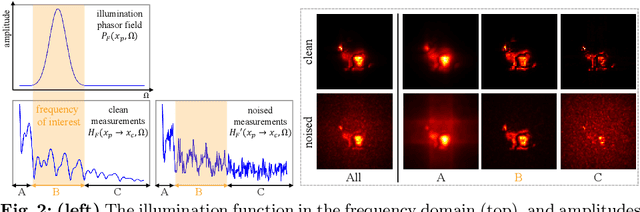
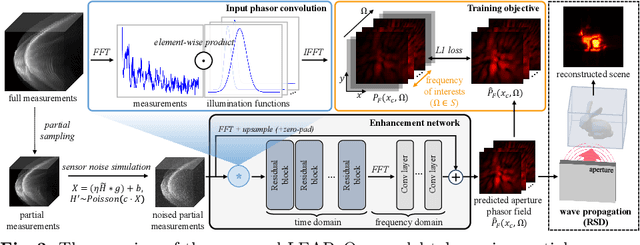
This paper aims to facilitate more practical NLOS imaging by reducing the number of samplings and scan areas. To this end, we introduce a phasor-based enhancement network that is capable of predicting clean and full measurements from noisy partial observations. We leverage a denoising autoencoder scheme to acquire rich and noise-robust representations in the measurement space. Through this pipeline, our enhancement network is trained to accurately reconstruct complete measurements from their corrupted and partial counterparts. However, we observe that the \naive application of denoising often yields degraded and over-smoothed results, caused by unnecessary and spurious frequency signals present in measurements. To address this issue, we introduce a phasor-based pipeline designed to limit the spectrum of our network to the frequency range of interests, where the majority of informative signals are detected. The phasor wavefronts at the aperture, which are band-limited signals, are employed as inputs and outputs of the network, guiding our network to learn from the frequency range of interests and discard unnecessary information. The experimental results in more practical acquisition scenarios demonstrate that we can look around the corners with $16\times$ or $64\times$ fewer samplings and $4\times$ smaller apertures. Our code is available at https://github.com/join16/LEAP.

Domain Reduction Strategy for Non Line of Sight Imaging

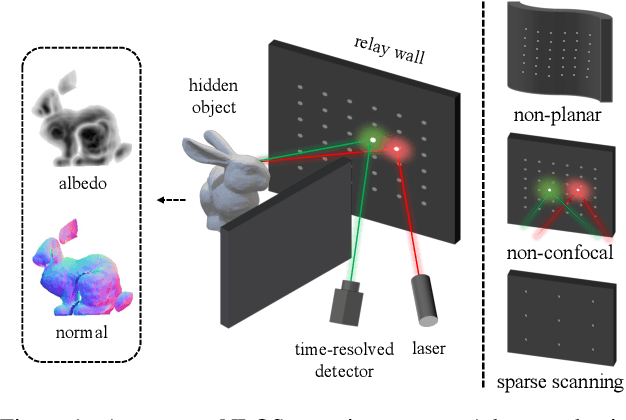
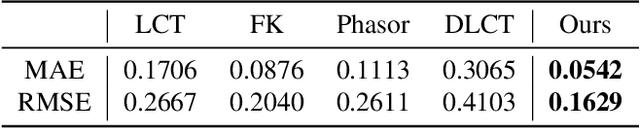
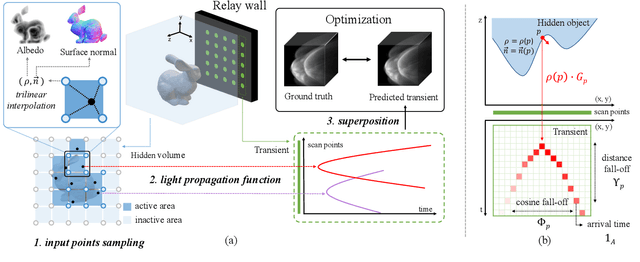
This paper presents a novel optimization-based method for non-line-of-sight (NLOS) imaging that aims to reconstruct hidden scenes under various setups. Our method is built upon the observation that photons returning from each point in hidden volumes can be independently computed if the interactions between hidden surfaces are trivially ignored. We model the generalized light propagation function to accurately represent the transients as a linear combination of these functions. Moreover, our proposed method includes a domain reduction procedure to exclude empty areas of the hidden volumes from the set of propagation functions, thereby improving computational efficiency of the optimization. We demonstrate the effectiveness of the method in various NLOS scenarios, including non-planar relay wall, sparse scanning patterns, confocal and non-confocal, and surface geometry reconstruction. Experiments conducted on both synthetic and real-world data clearly support the superiority and the efficiency of the proposed method in general NLOS scenarios.