Hyukjun Gweon
Nearest Labelset Using Double Distances for Multi-label Classification
Feb 15, 2017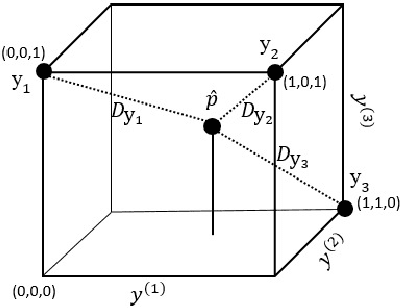
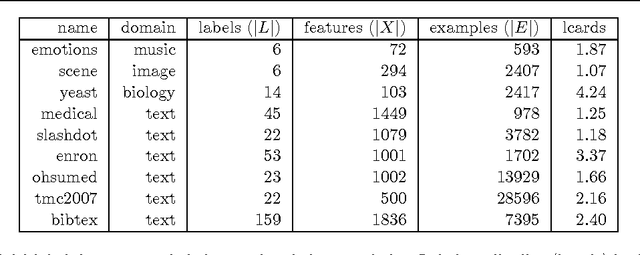
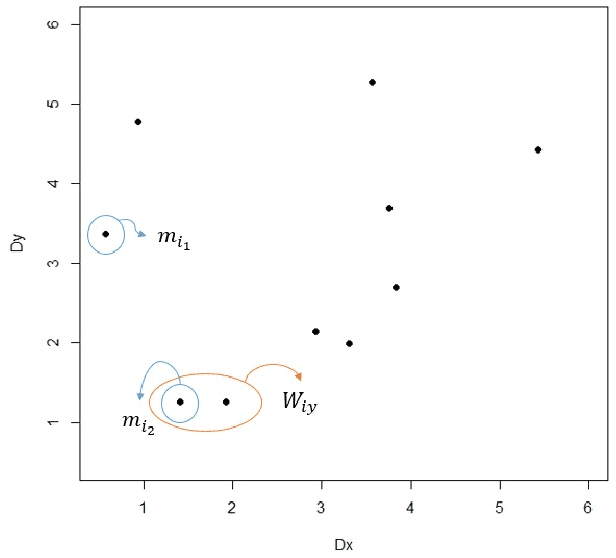
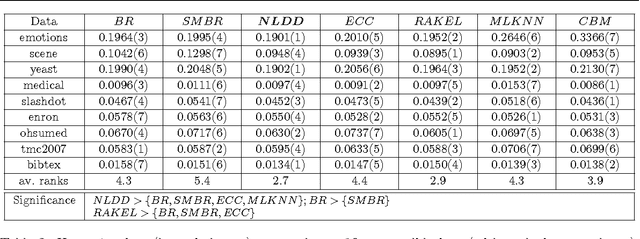
Abstract:Multi-label classification is a type of supervised learning where an instance may belong to multiple labels simultaneously. Predicting each label independently has been criticized for not exploiting any correlation between labels. In this paper we propose a novel approach, Nearest Labelset using Double Distances (NLDD), that predicts the labelset observed in the training data that minimizes a weighted sum of the distances in both the feature space and the label space to the new instance. The weights specify the relative tradeoff between the two distances. The weights are estimated from a binomial regression of the number of misclassified labels as a function of the two distances. Model parameters are estimated by maximum likelihood. NLDD only considers labelsets observed in the training data, thus implicitly taking into account label dependencies. Experiments on benchmark multi-label data sets show that the proposed method on average outperforms other well-known approaches in terms of Hamming loss, 0/1 loss, and multi-label accuracy and ranks second after ECC on the F-measure.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge