Hyeong In Choi
Seeded Ising Model and Statistical Natures of Human Iris Templates
Jan 03, 2018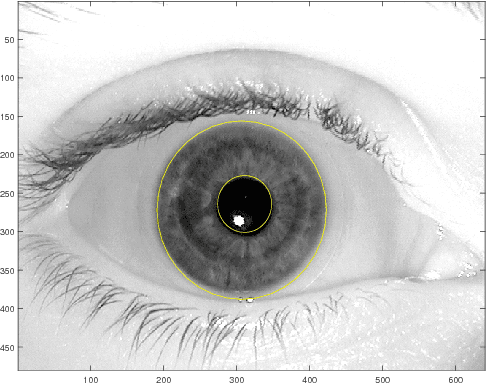
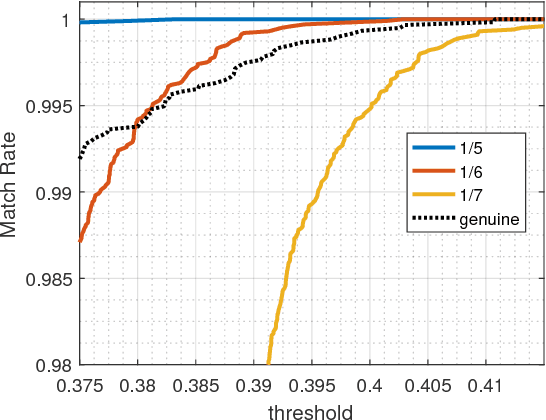
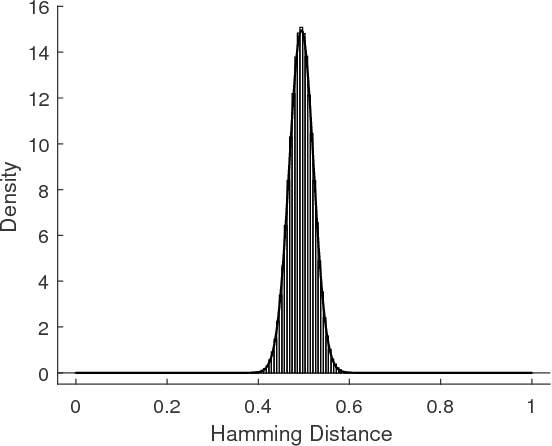
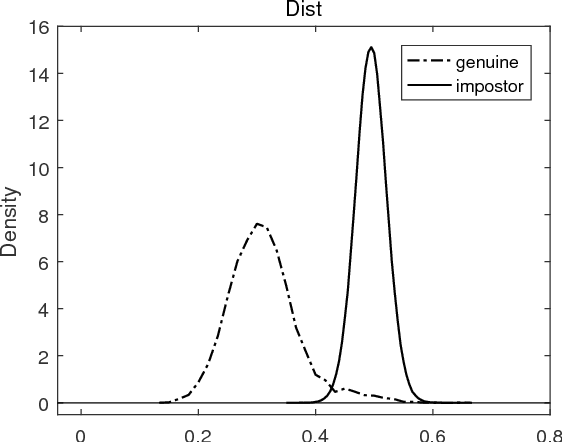
Abstract:We propose a variant of Ising model, called the Seeded Ising Model, to model probabilistic nature of human iris templates. This model is an Ising model in which the values at certain lattice points are held fixed throughout Ising model evolution. Using this we show how to reconstruct the full iris template from partial information, and we show that about 1/6 of the given template is needed to recover almost all information content of the original one in the sense that the resulting Hamming distance is well within the range to assert correctly the identity of the subject. This leads us to propose the concept of effective statistical degree of freedom of iris templates and show it is about 1/6 of the total number of bits. In particular, for a template of $2048$ bits, its effective statistical degree of freedom is about $342$ bits, which coincides very well with the degree of freedom computed by the completely different method proposed by Daugman.
* 7 pages
Continuous Semantic Topic Embedding Model Using Variational Autoencoder
Nov 24, 2017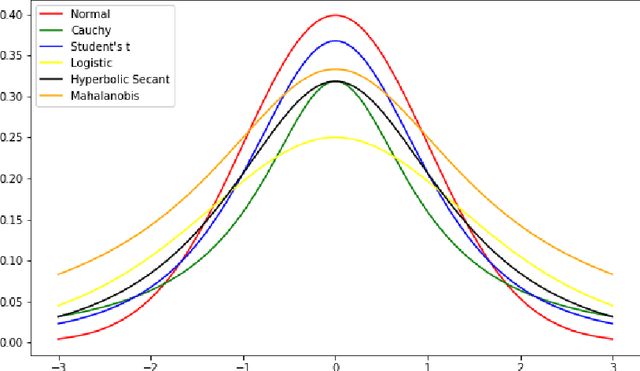

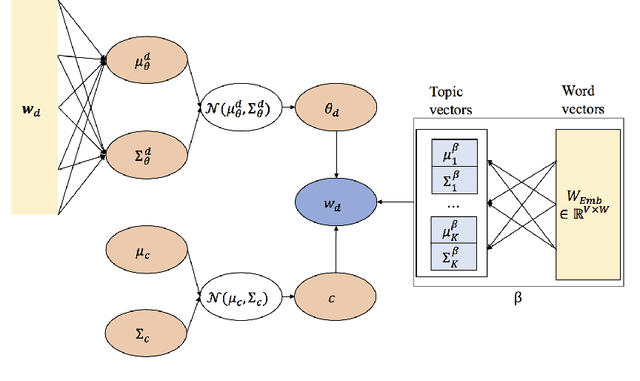
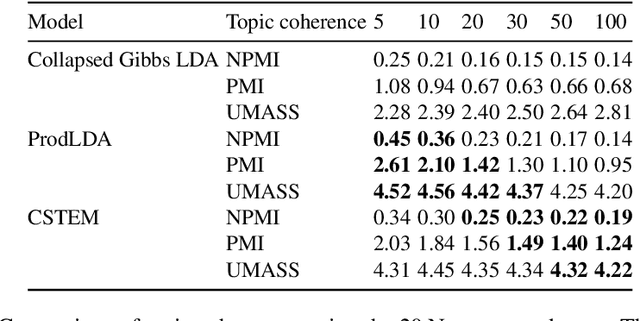
Abstract:This paper proposes the continuous semantic topic embedding model (CSTEM) which finds latent topic variables in documents using continuous semantic distance function between the topics and the words by means of the variational autoencoder(VAE). The semantic distance could be represented by any symmetric bell-shaped geometric distance function on the Euclidean space, for which the Mahalanobis distance is used in this paper. In order for the semantic distance to perform more properly, we newly introduce an additional model parameter for each word to take out the global factor from this distance indicating how likely it occurs regardless of its topic. It certainly improves the problem that the Gaussian distribution which is used in previous topic model with continuous word embedding could not explain the semantic relation correctly and helps to obtain the higher topic coherence. Through the experiments with the dataset of 20 Newsgroup, NIPS papers and CNN/Dailymail corpus, the performance of the recent state-of-the-art models is accomplished by our model as well as generating topic embedding vectors which makes possible to observe where the topic vectors are embedded with the word vectors in the real Euclidean space and how the topics are related each other semantically.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge