Hunter Scott Heidenreich
EigenNoise: A Contrastive Prior to Warm-Start Representations
May 09, 2022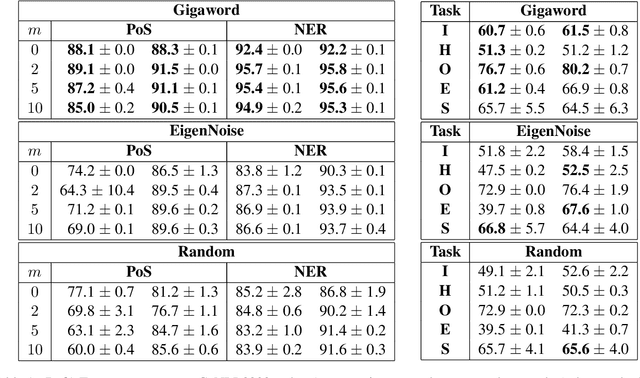
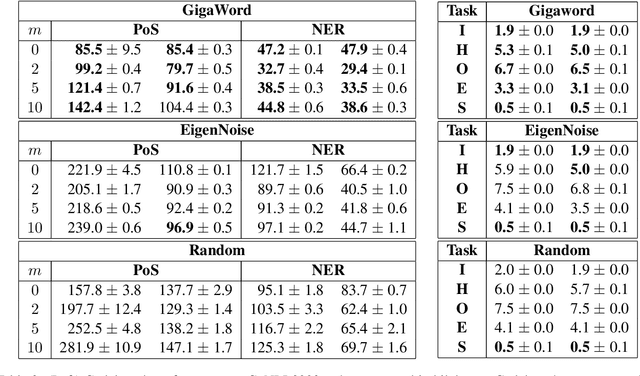
Abstract:In this work, we present a naive initialization scheme for word vectors based on a dense, independent co-occurrence model and provide preliminary results that suggest it is competitive and warrants further investigation. Specifically, we demonstrate through information-theoretic minimum description length (MDL) probing that our model, EigenNoise, can approach the performance of empirically trained GloVe despite the lack of any pre-training data (in the case of EigenNoise). We present these preliminary results with interest to set the stage for further investigations into how this competitive initialization works without pre-training data, as well as to invite the exploration of more intelligent initialization schemes informed by the theory of harmonic linguistic structure. Our application of this theory likewise contributes a novel (and effective) interpretation of recent discoveries which have elucidated the underlying distributional information that linguistic representations capture from data and contrast distributions.
To Know by the Company Words Keep and What Else Lies in the Vicinity
Apr 30, 2022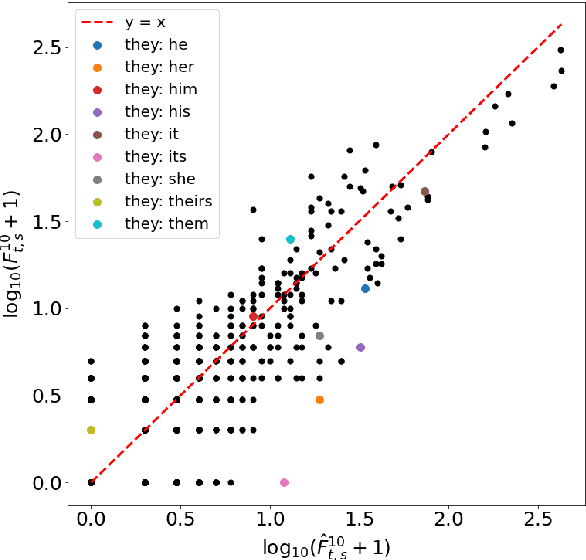

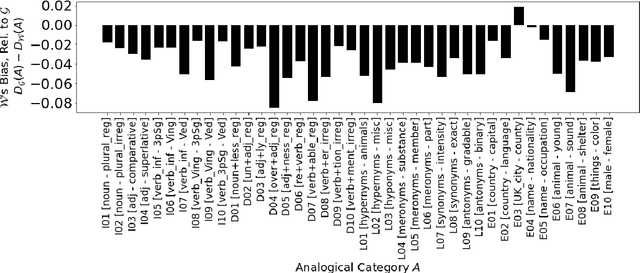
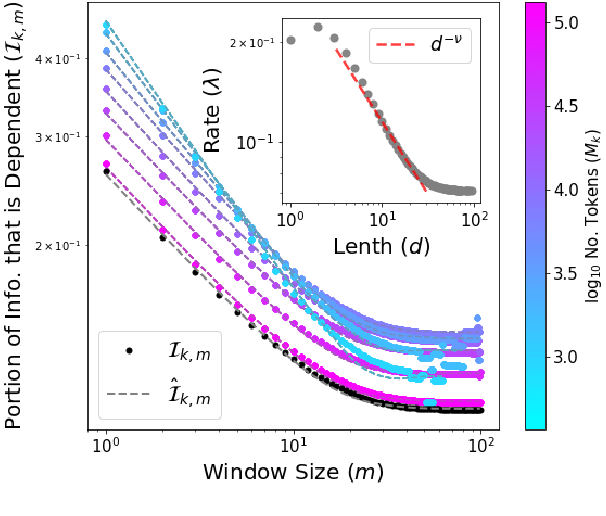
Abstract:The development of state-of-the-art (SOTA) Natural Language Processing (NLP) systems has steadily been establishing new techniques to absorb the statistics of linguistic data. These techniques often trace well-known constructs from traditional theories, and we study these connections to close gaps around key NLP methods as a means to orient future work. For this, we introduce an analytic model of the statistics learned by seminal algorithms (including GloVe and Word2Vec), and derive insights for systems that use these algorithms and the statistics of co-occurrence, in general. In this work, we derive -- to the best of our knowledge -- the first known solution to Word2Vec's softmax-optimized, skip-gram algorithm. This result presents exciting potential for future development as a direct solution to a deep learning (DL) language model's (LM's) matrix factorization. However, we use the solution to demonstrate a seemingly-universal existence of a property that word vectors exhibit and which allows for the prophylactic discernment of biases in data -- prior to their absorption by DL models. To qualify our work, we conduct an analysis of independence, i.e., on the density of statistical dependencies in co-occurrence models, which in turn renders insights on the distributional hypothesis' partial fulfillment by co-occurrence statistics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge