Huiyue Yi
Double criterion-based estimator for signal number estimation for the colored noise with unknown covariance matrix
Nov 23, 2022Abstract:The subspace-based techniques are widely utilized to estimate the parameters of sums of complex sinusoids corrupted by noise, and the zoom ESPRIT algorithm utilizes the zoom technique to apply the ESPRIT to a narrow frequency band to improve the accuracy of frequency estimation. However, the Gaussian noise becomes non-Gaussian in the zoomed baseband after being filtered by a low-pass filter, and thus has an unknown covariance matrix. However, most exiting algorithms for model order estimation performs poorly for the case of colored noise with unknown covariance matrix. In order to accurately estimate the dimension of the signal subspace for the zoom ESPRIT algorithm, this paper proposes a novel strategy to estimate the number of signals for the case of colored noise with unknown covariance matrix. The proposed strategy is based on the analysis of the behavior of information theoretic criteria utilized in model order selection. Firstly, a first criterion is defined as the ratio of the current eigenvalue and the mean of the next ones, and its properties is analyzed with respect to the over-modeling and under-modeling. Secondly, a novel second criterion is designed as the ratio of the current value and the next value of the first criterion, and its properties is also analyzed with respect to the over-modeling and under-modeling. Then, a novel signal number estimation method is proposed by combining the second criterion with the first criterion to check whether the eigenvalue being tested is arising from a signal or from noise. The resulted signal number estimation method is called as the double criterion-based estimator as it utilizes two criteria to separate the signal eigenvalues from the noise eigenvalues. Finally, simulation results are presented to illustrate the performance of the proposed double criterion-based estimator and compare it with the existing methods.
Iterative Adaptively Regularized LASSO-ADMM Algorithm for CFAR Estimation of Sparse Signals: IAR-LASSO-ADMM-CFAR Algorithm
Aug 24, 2022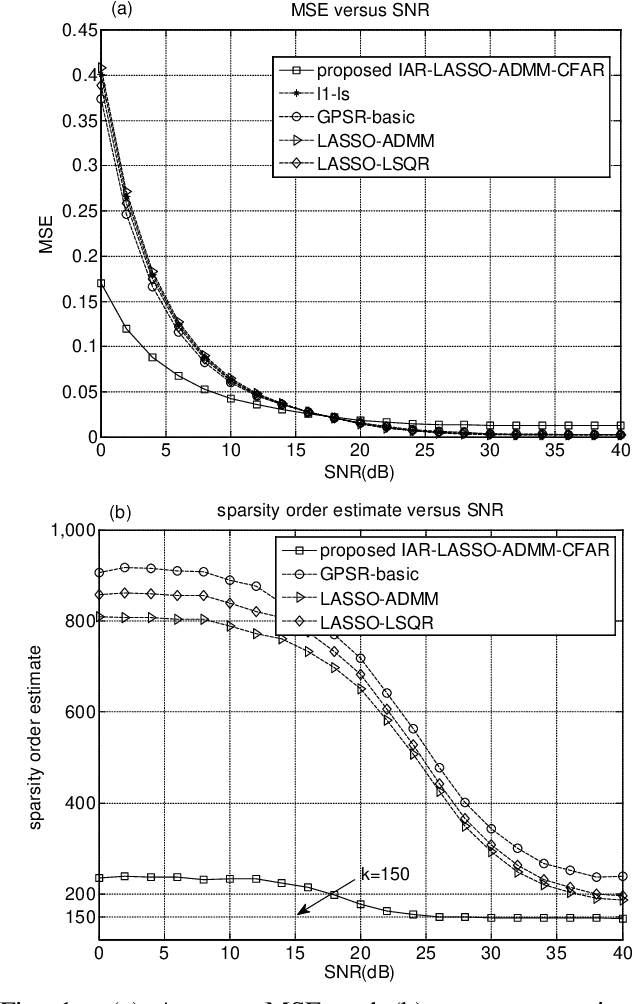
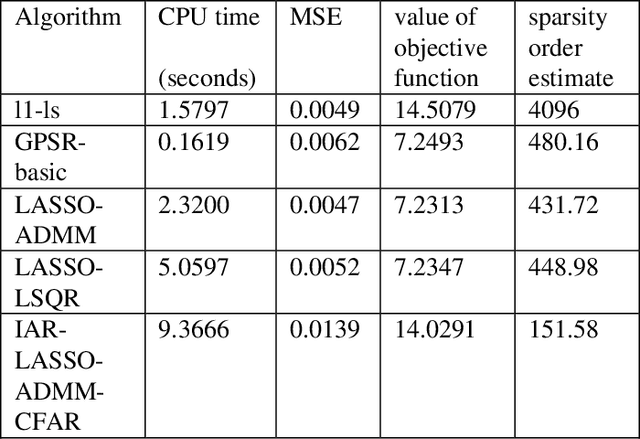
Abstract:The least-absolute shrinkage and selection operator (LASSO) is a regularization technique for estimating sparse signals of interest emerging in various applications and can be efficiently solved via the alternating direction method of multipliers (ADMM), which will be termed as LASSO-ADMM algorithm. The choice of the regularization parameter has significant impact on the performance of LASSO-ADMM algorithm. However, the optimization for the regularization parameter in the existing LASSO-ADMM algorithms has not been solved yet. In order to optimize this regularization parameter, we propose an efficient iterative adaptively regularized LASSO-ADMM (IAR-LASSO-ADMM) algorithm by iteratively updating the regularization parameter in the LASSO-ADMM algorithm. Moreover, a method is designed to iteratively update the regularization parameter by adding an outer iteration to the LASSO-ADMM algorithm. Specifically, at each outer iteration the zero support of the estimate obtained by the inner LASSO-ADMM algorithm is utilized to estimate the noise variance, and the noise variance is utilized to update the threshold according to a pre-defined const false alarm rate (CFAR). Then, the resulting threshold is utilized to update both the non-zero support of the estimate and the regularization parameter, and proceed to the next inner iteration. In addition, a suitable stopping criterion is designed to terminate the outer iteration process to obtain the final non-zero support of the estimate of the sparse measurement signals. The resulting algorithm is termed as IAR-LASSO-ADMM-CFAR algorithm. Finally, simulation results have been presented to show that the proposed IAR-LASSO-ADMM-CFAR algorithm outperforms the conventional LASSO-ADMM algorithm and other existing algorithms in terms of reconstruction accuracy, and its sparsity order estimate is more accurate than the existing algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge