Hsiao-Dong Chiang
Adaptive Learning Rate and Momentum for Training Deep Neural Networks
Jun 22, 2021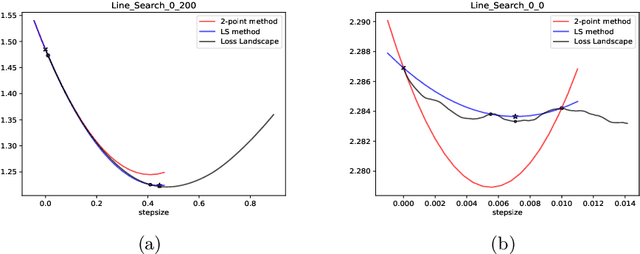
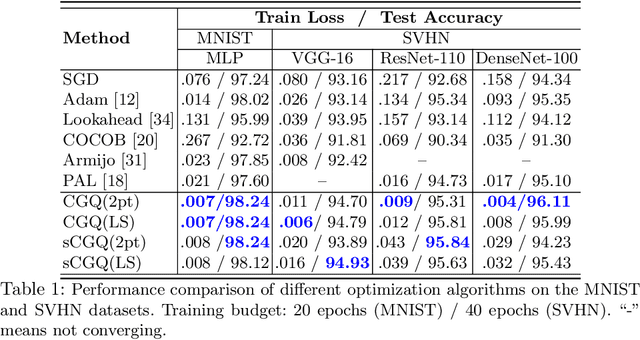
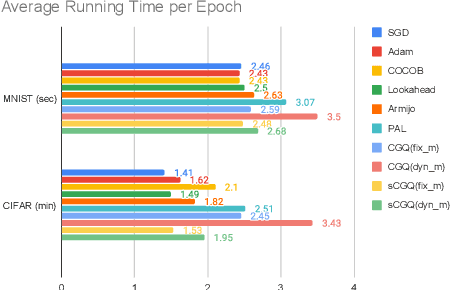
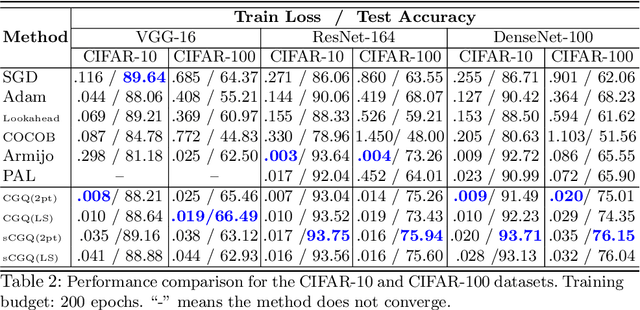
Abstract:Recent progress on deep learning relies heavily on the quality and efficiency of training algorithms. In this paper, we develop a fast training method motivated by the nonlinear Conjugate Gradient (CG) framework. We propose the Conjugate Gradient with Quadratic line-search (CGQ) method. On the one hand, a quadratic line-search determines the step size according to current loss landscape. On the other hand, the momentum factor is dynamically updated in computing the conjugate gradient parameter (like Polak-Ribiere). Theoretical results to ensure the convergence of our method in strong convex settings is developed. And experiments in image classification datasets show that our method yields faster convergence than other local solvers and has better generalization capability (test set accuracy). One major advantage of the paper method is that tedious hand tuning of hyperparameters like the learning rate and momentum is avoided.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge