Hristo Paskov
Learning High Order Feature Interactions with Fine Control Kernels
Feb 09, 2020
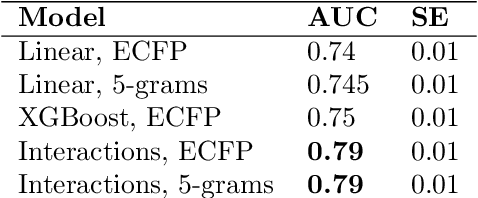
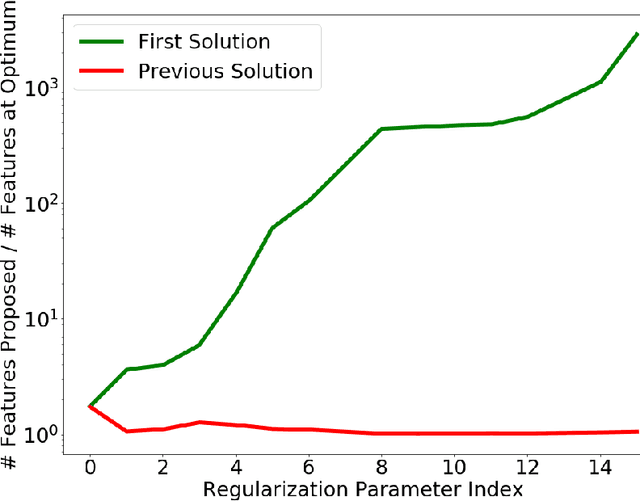

Abstract:We provide a methodology for learning sparse statistical models that use as features all possible multiplicative interactions among an underlying atomic set of features. While the resulting optimization problems are exponentially sized, our methodology leads to algorithms that can often solve these problems exactly or provide approximate solutions based on combining highly correlated features. We also introduce an algorithmic paradigm, the Fine Control Kernel framework, so named because it is based on Fenchel Duality and is reminiscent of kernel methods. Its theory is tailored to large sparse learning problems, and it leads to efficient feature screening rules for interactions. These rules are inspired by the Apriori algorithm for market basket analysis -- which also falls under the purview of Fine Control Kernels, and can be applied to a plurality of learning problems including the Lasso and sparse matrix estimation. Experiments on biomedical datasets demonstrate the efficacy of our methodology in deriving algorithms that efficiently produce interactions models which achieve state-of-the-art accuracy and are interpretable.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge