GPCR-Filter: a deep learning framework for efficient and precise GPCR modulator discovery

G protein-coupled receptors (GPCRs) govern diverse physiological processes and are central to modern pharmacology. Yet discovering GPCR modulators remains challenging because receptor activation often arises from complex allosteric effects rather than direct binding affinity, and conventional assays are slow, costly, and not optimized for capturing these dynamics. Here we present GPCR-Filter, a deep learning framework specifically developed for GPCR modulator discovery. We assembled a high-quality dataset of over 90,000 experimentally validated GPCR-ligand pairs, providing a robust foundation for training and evaluation. GPCR-Filter integrates the ESM-3 protein language model for high-fidelity GPCR sequence representations with graph neural networks that encode ligand structures, coupled through an attention-based fusion mechanism that learns receptor-ligand functional relationships. Across multiple evaluation settings, GPCR-Filter consistently outperforms state-of-the-art compound-protein interaction models and exhibits strong generalization to unseen receptors and ligands. Notably, the model successfully identified micromolar-level agonists of the 5-HT\textsubscript{1A} receptor with distinct chemical frameworks. These results establish GPCR-Filter as a scalable and effective computational approach for GPCR modulator discovery, advancing AI-assisted drug development for complex signaling systems.

Tensor p-shrinkage nuclear norm for low-rank tensor completion

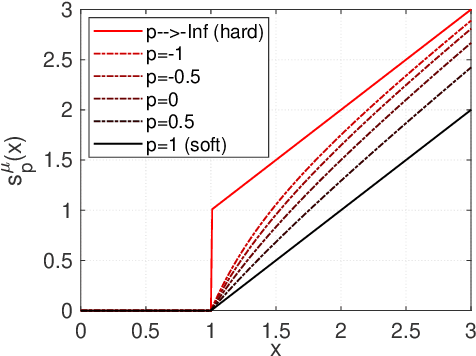
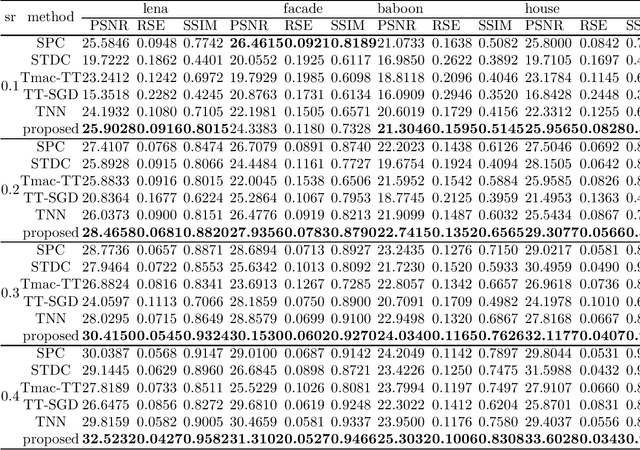
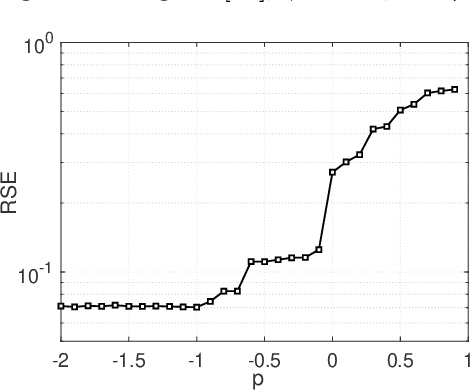
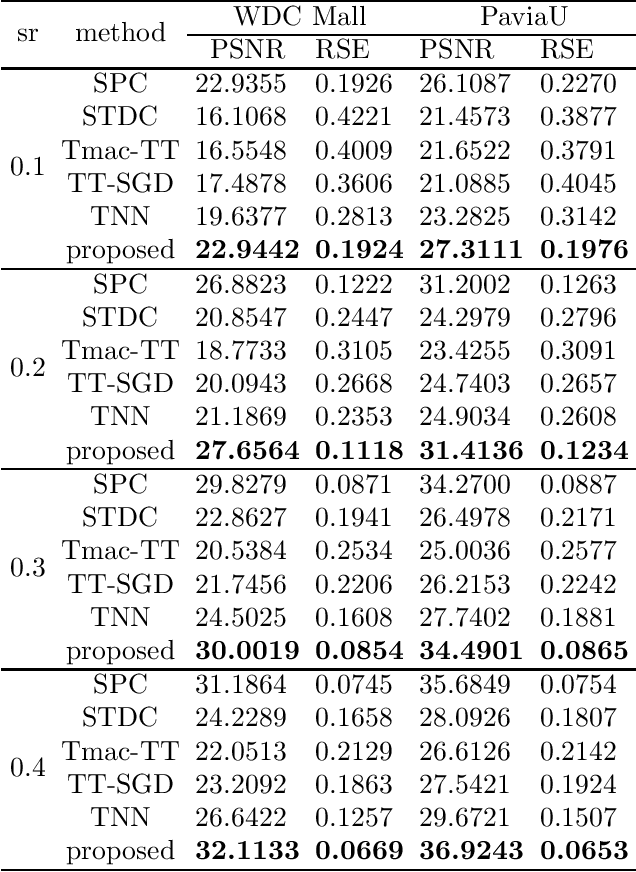
In this paper, a new definition of tensor p-shrinkage nuclear norm (p-TNN) is proposed based on tensor singular value decomposition (t-SVD). In particular, it can be proved that p-TNN is a better approximation of the tensor average rank than the tensor nuclear norm when p < 1. Therefore, by employing the p-shrinkage nuclear norm, a novel low-rank tensor completion (LRTC) model is proposed to estimate a tensor from its partial observations. Statistically, the upper bound of recovery error is provided for the LRTC model. Furthermore, an efficient algorithm, accelerated by the adaptive momentum scheme, is developed to solve the resulting nonconvex optimization problem. It can be further guaranteed that the algorithm enjoys a global convergence rate under the smoothness assumption. Numerical experiments conducted on both synthetic and real-world data sets verify our results and demonstrate the superiority of our p-TNN in LRTC problems over several state-of-the-art methods.