Tensor p-shrinkage nuclear norm for low-rank tensor completion
Paper and Code
Jul 09, 2019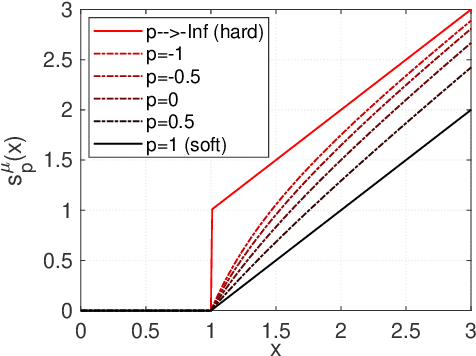
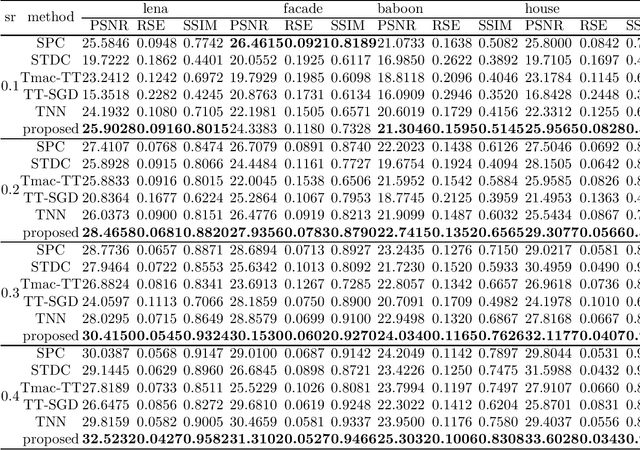
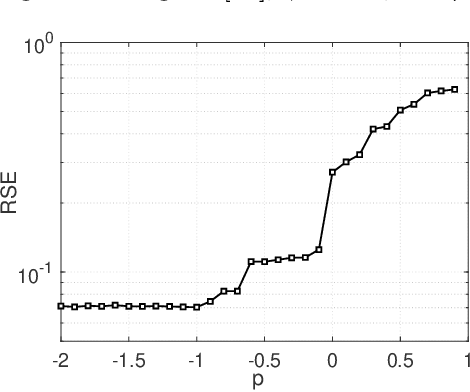
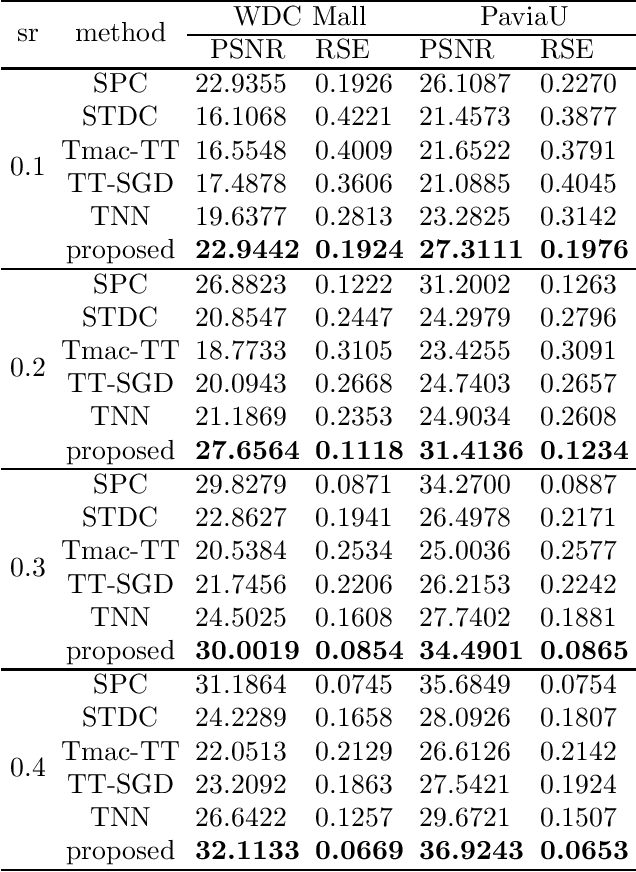
In this paper, a new definition of tensor p-shrinkage nuclear norm (p-TNN) is proposed based on tensor singular value decomposition (t-SVD). In particular, it can be proved that p-TNN is a better approximation of the tensor average rank than the tensor nuclear norm when p < 1. Therefore, by employing the p-shrinkage nuclear norm, a novel low-rank tensor completion (LRTC) model is proposed to estimate a tensor from its partial observations. Statistically, the upper bound of recovery error is provided for the LRTC model. Furthermore, an efficient algorithm, accelerated by the adaptive momentum scheme, is developed to solve the resulting nonconvex optimization problem. It can be further guaranteed that the algorithm enjoys a global convergence rate under the smoothness assumption. Numerical experiments conducted on both synthetic and real-world data sets verify our results and demonstrate the superiority of our p-TNN in LRTC problems over several state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge