Hiro Gangi
Bayesian Optimization that Limits Search Region to Lower Dimensions Utilizing Local GPR
Mar 13, 2024
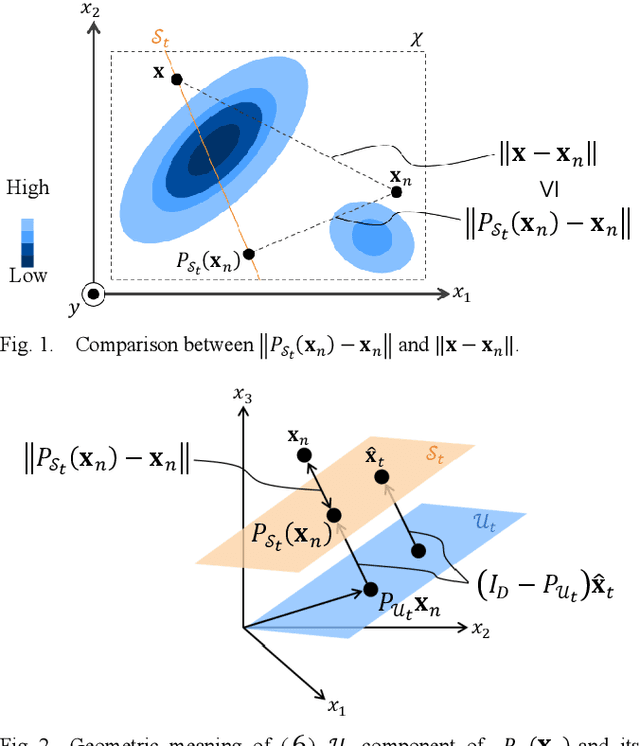
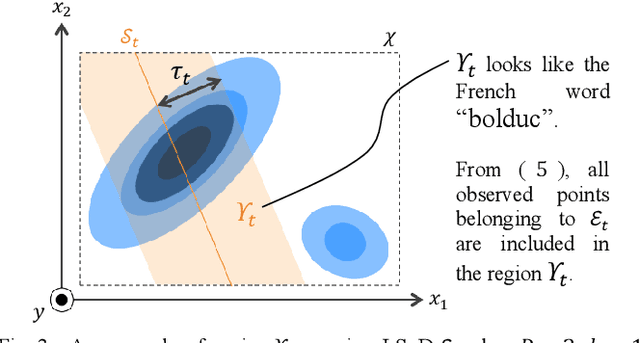
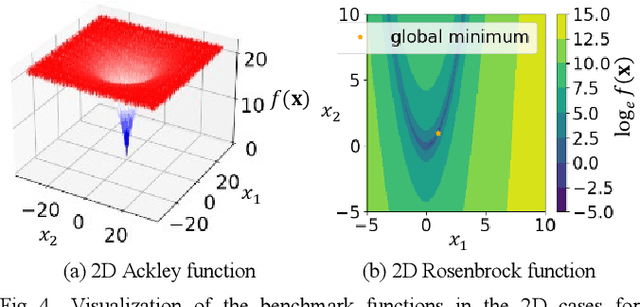
Abstract:Optimization of product and system characteristics is required in many fields, including design and control. Bayesian optimization (BO) is often used when there are high observing costs, because BO theoretically guarantees an upper bound on regret. However, computational costs increase exponentially with the number of parameters to be optimized, decreasing search efficiency. We propose a BO that limits the search region to lower dimensions and utilizes local Gaussian process regression (LGPR) to scale the BO to higher dimensions. LGPR treats the low-dimensional search region as "local," improving prediction accuracies there. The LGPR model is trained on a local subset of data specific to that region. This improves prediction accuracy and search efficiency and reduces the time complexity of matrix inversion in the Gaussian process regression. In evaluations with 20D Ackley and Rosenbrock functions, search efficiencies are equal to or higher than those of the compared methods, improved by about 69% and 40% from the case without LGPR. We apply our method to an automatic design task for a power semiconductor device. We successfully reduce the specific on-resistance to 25% better than a conventional method and 3.4% better than without LGPR.
* 8 pages, 13 figures, 22nd International Conference on Machine Learning and Applications (ICMLA2023)
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge