Herman Schmit
Direct Spatial Implementation of Sparse Matrix Multipliers for Reservoir Computing
Jan 21, 2021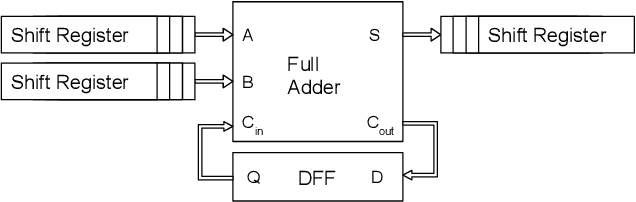
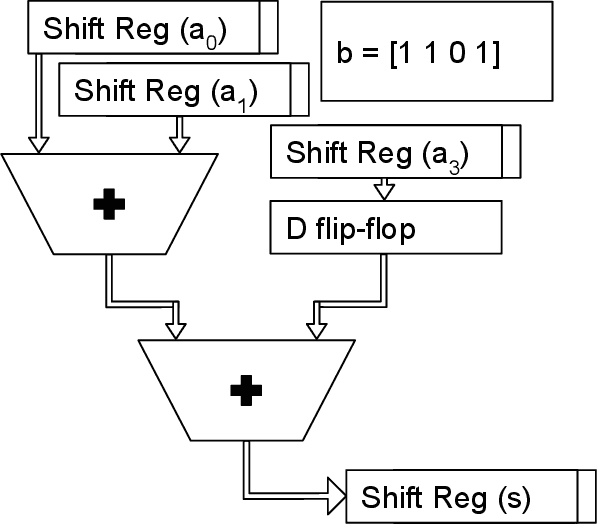
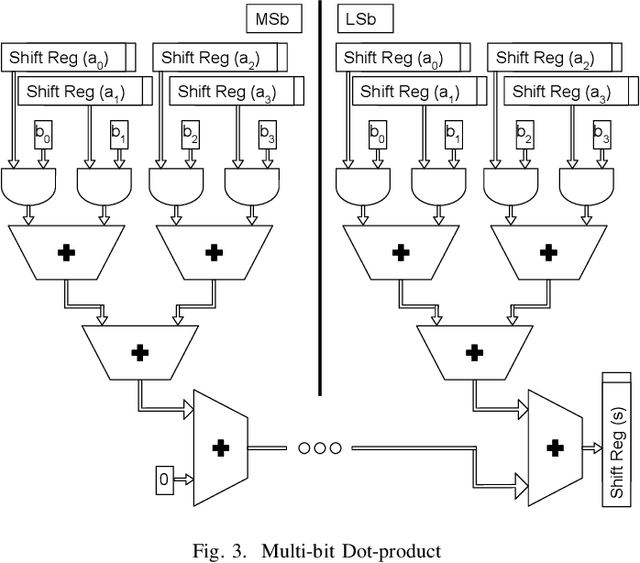
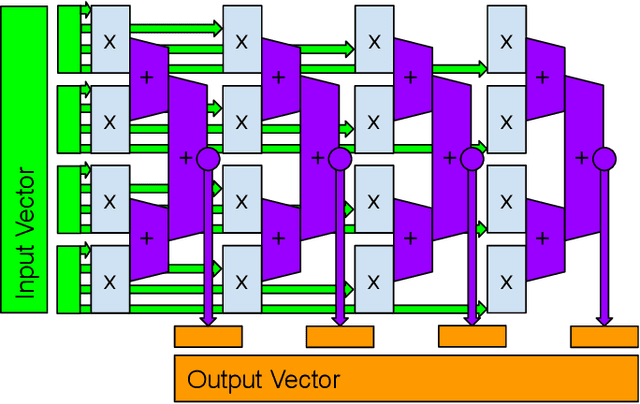
Abstract:Reservoir computing systems rely on the recurrent multiplication of a very large, sparse, fixed matrix. We argue that direct spatial implementation of these fixed matrices minimizes the work performed in the computation, and allows for significant reduction in latency and power through constant propagation and logic minimization. Bit-serial arithmetic enables massive static matrices to be implemented. We present the structure of our bit-serial matrix multiplier, and evaluate using canonical signed digit representation to further reduce logic utilization. We have implemented these matrices on a large FPGA and provide a cost model that is simple and extensible. These FPGA implementations, on average, reduce latency by 50x up to 86x versus GPU libraries. Comparing against a recent sparse DNN accelerator, we measure a 4.1x to 47x reduction in latency depending on matrix dimension and sparsity. Throughput of the FPGA solution is also competitive for a wide range of matrix dimensions and batch sizes. Finally, we discuss ways these techniques could be deployed in ASICs, making them applicable for dynamic sparse matrix computations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge