Henrik Forssell
On Equivalence and Cores for Incomplete Databases in Open and Closed Worlds
Jan 14, 2020Abstract:Data exchange heavily relies on the notion of incomplete database instances. Several semantics for such instances have been proposed and include open (OWA), closed (CWA), and open-closed (OCWA) world. For all these semantics important questions are: whether one incomplete instance semantically implies another; when two are semantically equivalent; and whether a smaller or smallest semantically equivalent instance exists. For OWA and CWA these questions are fully answered. For several variants of OCWA, however, they remain open. In this work we adress these questions for Closed Powerset semantics and the OCWA semantics of Libkin and Sirangelo, 2011. We define a new OCWA semantics, called OCWA*, in terms of homomorphic covers that subsumes both semantics, and characterize semantic implication and equivalence in terms of such covers. This characterization yields a guess-and-check algorithm to decide equivalence, and shows that the problem is NP-complete. For the minimization problem we show that for several common notions of minimality there is in general no unique minimal equivalent instance for Closed Powerset semantics, and consequently not for the more expressive OCWA* either. However, for Closed Powerset semantics we show that one can find, for any incomplete database, a unique finite set of its subinstances which are subinstances (up to renaming of nulls) of all instances semantically equivalent to the original incomplete one. We study properties of this set, and extend the analysis to OCWA*.
Generating Ontologies from Templates: A Rule-Based Approach for Capturing Regularity
Sep 27, 2018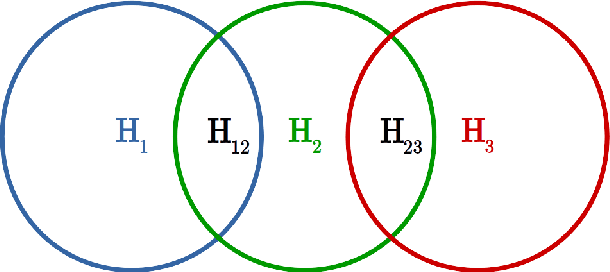
Abstract:We present a second-order language that can be used to succinctly specify ontologies in a consistent and transparent manner. This language is based on ontology templates (OTTR), a framework for capturing recurring patterns of axioms in ontological modelling. The language and our results are independent of any specific DL. We define the language and its semantics, including the case of negation-as-failure, investigate reasoning over ontologies specified using our language, and show results about the decidability of useful reasoning tasks about the language itself. We also state and discuss some open problems that we believe to be of interest.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge