Distal Interference: Exploring the Limits of Model-Based Continual Learning

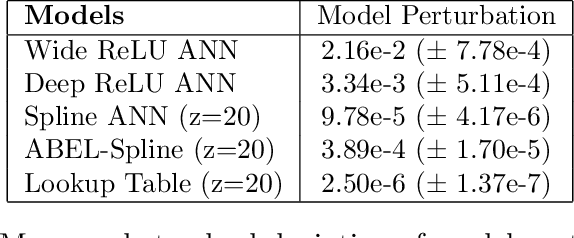
Continual learning is the sequential learning of different tasks by a machine learning model. Continual learning is known to be hindered by catastrophic interference or forgetting, i.e. rapid unlearning of earlier learned tasks when new tasks are learned. Despite their practical success, artificial neural networks (ANNs) are prone to catastrophic interference. This study analyses how gradient descent and overlapping representations between distant input points lead to distal interference and catastrophic interference. Distal interference refers to the phenomenon where training a model on a subset of the domain leads to non-local changes on other subsets of the domain. This study shows that uniformly trainable models without distal interference must be exponentially large. A novel antisymmetric bounded exponential layer B-spline ANN architecture named ABEL-Spline is proposed that can approximate any continuous function, is uniformly trainable, has polynomial computational complexity, and provides some guarantees for distal interference. Experiments are presented to demonstrate the theoretical properties of ABEL-Splines. ABEL-Splines are also evaluated on benchmark regression problems. It is concluded that the weaker distal interference guarantees in ABEL-Splines are insufficient for model-only continual learning. It is conjectured that continual learning with polynomial complexity models requires augmentation of the training data or algorithm.

Cauchy Loss Function: Robustness Under Gaussian and Cauchy Noise

In supervised machine learning, the choice of loss function implicitly assumes a particular noise distribution over the data. For example, the frequently used mean squared error (MSE) loss assumes a Gaussian noise distribution. The choice of loss function during training and testing affects the performance of artificial neural networks (ANNs). It is known that MSE may yield substandard performance in the presence of outliers. The Cauchy loss function (CLF) assumes a Cauchy noise distribution, and is therefore potentially better suited for data with outliers. This papers aims to determine the extent of robustness and generalisability of the CLF as compared to MSE. CLF and MSE are assessed on a few handcrafted regression problems, and a real-world regression problem with artificially simulated outliers, in the context of ANN training. CLF yielded results that were either comparable to or better than the results yielded by MSE, with a few notable exceptions.

ATLAS: Universal Function Approximator for Memory Retention

Artificial neural networks (ANNs), despite their universal function approximation capability and practical success, are subject to catastrophic forgetting. Catastrophic forgetting refers to the abrupt unlearning of a previous task when a new task is learned. It is an emergent phenomenon that hinders continual learning. Existing universal function approximation theorems for ANNs guarantee function approximation ability, but do not predict catastrophic forgetting. This paper presents a novel universal approximation theorem for multi-variable functions using only single-variable functions and exponential functions. Furthermore, we present ATLAS: a novel ANN architecture based on the new theorem. It is shown that ATLAS is a universal function approximator capable of some memory retention, and continual learning. The memory of ATLAS is imperfect, with some off-target effects during continual learning, but it is well-behaved and predictable. An efficient implementation of ATLAS is provided. Experiments are conducted to evaluate both the function approximation and memory retention capabilities of ATLAS.

KASAM: Spline Additive Models for Function Approximation

Neural networks have been criticised for their inability to perform continual learning due to catastrophic forgetting and rapid unlearning of a past concept when a new concept is introduced. Catastrophic forgetting can be alleviated by specifically designed models and training techniques. This paper outlines a novel Spline Additive Model (SAM). SAM exhibits intrinsic memory retention with sufficient expressive power for many practical tasks, but is not a universal function approximator. SAM is extended with the Kolmogorov-Arnold representation theorem to a novel universal function approximator, called the Kolmogorov-Arnold Spline Additive Model - KASAM. The memory retention, expressive power and limitations of SAM and KASAM are illustrated analytically and empirically. SAM exhibited robust but imperfect memory retention, with small regions of overlapping interference in sequential learning tasks. KASAM exhibited greater susceptibility to catastrophic forgetting. KASAM in combination with pseudo-rehearsal training techniques exhibited superior performance in regression tasks and memory retention.