Regret-Driven Portfolios: LLM-Guided Smart Clustering for Optimal Allocation

We attempt to mitigate the persistent tradeoff between risk and return in medium- to long-term portfolio management. This paper proposes a novel LLM-guided no-regret portfolio allocation framework that integrates online learning dynamics, market sentiment indicators, and large language model (LLM)-based hedging to construct high-Sharpe ratio portfolios tailored for risk-averse investors and institutional fund managers. Our approach builds on a follow-the-leader approach, enriched with sentiment-based trade filtering and LLM-driven downside protection. Empirical results demonstrate that our method outperforms a SPY buy-and-hold baseline by 69% in annualized returns and 119% in Sharpe ratio.

Path to Stochastic Stability: Comparative Analysis of Stochastic Learning Dynamics in Games

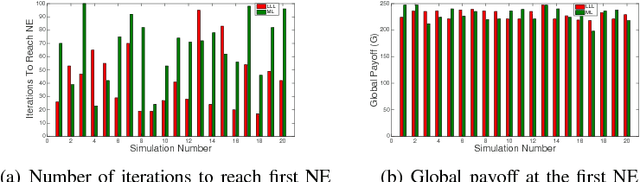
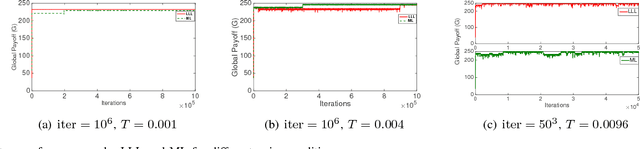
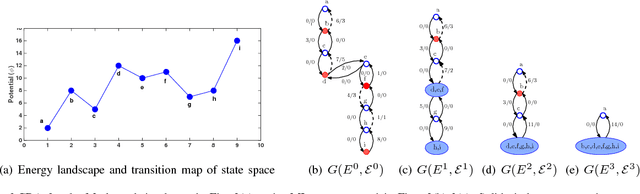
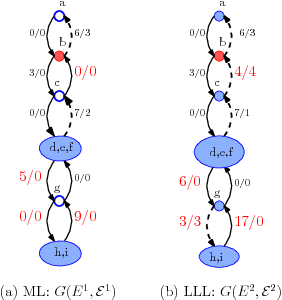
Stochastic stability is a popular solution concept for stochastic learning dynamics in games. However, a critical limitation of this solution concept is its inability to distinguish between different learning rules that lead to the same steady-state behavior. We address this limitation for the first time and develop a framework for the comparative analysis of stochastic learning dynamics with different update rules but same steady-state behavior. We present the framework in the context of two learning dynamics: Log-Linear Learning (LLL) and Metropolis Learning (ML). Although both of these dynamics have the same stochastically stable states, LLL and ML correspond to different behavioral models for decision making. Moreover, we demonstrate through an example setup of sensor coverage game that for each of these dynamics, the paths to stochastically stable states exhibit distinctive behaviors. Therefore, we propose multiple criteria to analyze and quantify the differences in the short and medium run behavior of stochastic learning dynamics. We derive and compare upper bounds on the expected hitting time to the set of Nash equilibria for both LLL and ML. For the medium to long-run behavior, we identify a set of tools from the theory of perturbed Markov chains that result in a hierarchical decomposition of the state space into collections of states called cycles. We compare LLL and ML based on the proposed criteria and develop invaluable insights into the comparative behavior of the two dynamics.