Harshvardhan
Stochastic Compositional Gradient Descent under Compositional constraints
Dec 17, 2020
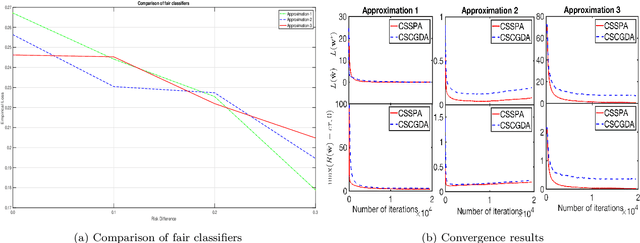

Abstract:This work studies constrained stochastic optimization problems where the objective and constraint functions are convex and expressed as compositions of stochastic functions. The problem arises in the context of fair classification, fair regression, and the design of queuing systems. Of particular interest is the large-scale setting where an oracle provides the stochastic gradients of the constituent functions, and the goal is to solve the problem with a minimal number of calls to the oracle. The problem arises in fair classification/regression and in the design of queuing systems. Owing to the compositional form, the stochastic gradients provided by the oracle do not yield unbiased estimates of the objective or constraint gradients. Instead, we construct approximate gradients by tracking the inner function evaluations, resulting in a quasi-gradient saddle point algorithm. We prove that the proposed algorithm is guaranteed to find the optimal and feasible solution almost surely. We further establish that the proposed algorithm requires $\mathcal{O}(1/\epsilon^4)$ data samples in order to obtain an $\epsilon$-approximate optimal point while also ensuring zero constraint violation. The result matches the sample complexity of the stochastic compositional gradient descent method for unconstrained problems and improves upon the best-known sample complexity results for the constrained settings. The efficacy of the proposed algorithm is tested on both fair classification and fair regression problems. The numerical results show that the proposed algorithm outperforms the state-of-the-art algorithms in terms of the convergence rate.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge