Robustness: a new SLIP model based criterion for gait transitions in bipedal locomotion

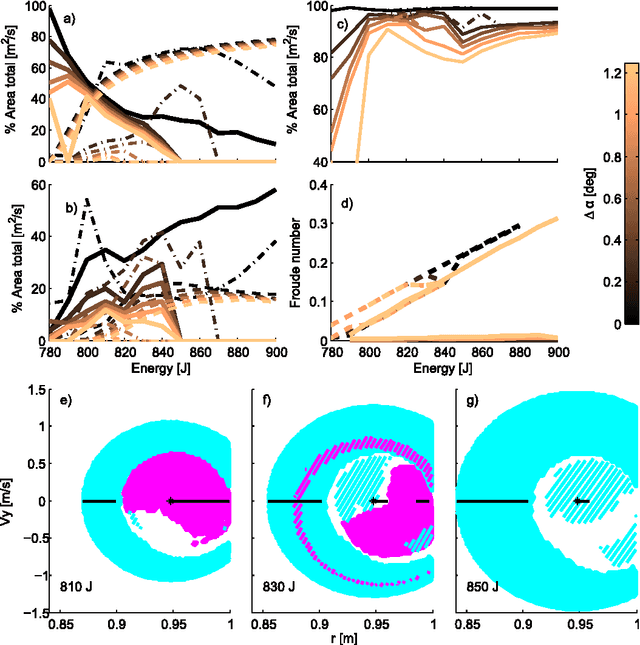
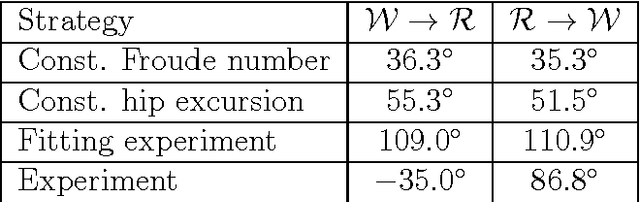
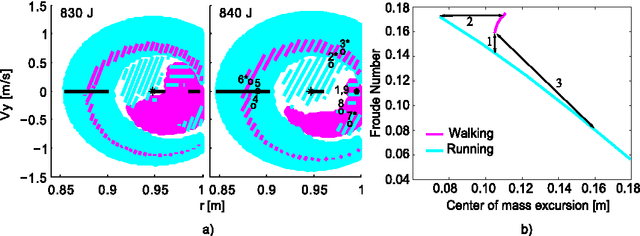
Bipedal locomotion is a phenomenon that still eludes a fundamental and concise mathematical understanding. Conceptual models that capture some relevant aspects of the process exist but their full explanatory power is not yet exhausted. In the current study, we introduce the robustness criterion which defines the conditions for stable locomotion when steps are taken with imprecise angle of attack. Intuitively, the necessity of a higher precision indicates the difficulty to continue moving with a given gait. We show that the spring-loaded inverted pendulum model, under the robustness criterion, is consistent with previously reported findings on attentional demand during human locomotion. This criterion allows transitions between running and walking, many of which conserve forward speed. Simulations of transitions predict Froude numbers below the ones observed in humans, nevertheless the model satisfactorily reproduces several biomechanical indicators such as hip excursion, gait duty factor and vertical ground reaction force profiles. Furthermore, we identify reversible robust walk-run transitions, which allow the system to execute a robust version of the hopping gait. These findings foster the spring-loaded inverted pendulum model as the unifying framework for the understanding of bipedal locomotion.

Exploiting the Passive Dynamics of a Compliant Leg to Develop Gait Transitions

In the area of bipedal locomotion, the spring loaded inverted pendulum (SLIP) model has been proposed as a unified framework to explain the dynamics of a wide variety of gaits. In this paper, we present a novel analysis of the mathematical model and its dynamical properties. We use the perspective of hybrid dynamical systems to study the dynamics and define concepts such as partial stability and viability. With this approach, on the one hand, we identified stable and unstable regions of locomotion. On the other hand, we found ways to exploit the unstable regions of locomotion to induce gait transitions at a constant energy regime. Additionally, we show that simple non-constant angle of attack control policies can render the system almost always stable.