Quantum Phase Recognition using Quantum Tensor Networks

Machine learning (ML) has recently facilitated many advances in solving problems related to many-body physical systems. Given the intrinsic quantum nature of these problems, it is natural to speculate that quantum-enhanced machine learning will enable us to unveil even greater details than we currently have. With this motivation, this paper examines a quantum machine learning approach based on shallow variational ansatz inspired by tensor networks for supervised learning tasks. In particular, we first look at the standard image classification tasks using the Fashion-MNIST dataset and study the effect of repeating tensor network layers on ansatz's expressibility and performance. Finally, we use this strategy to tackle the problem of quantum phase recognition for the transverse-field Ising and Heisenberg spin models in one and two dimensions, where we were able to reach $\geq 98\%$ test-set accuracies with both multi-scale entanglement renormalization ansatz (MERA) and tree tensor network (TTN) inspired parametrized quantum circuits.

Qubit Routing using Graph Neural Network aided Monte Carlo Tree Search

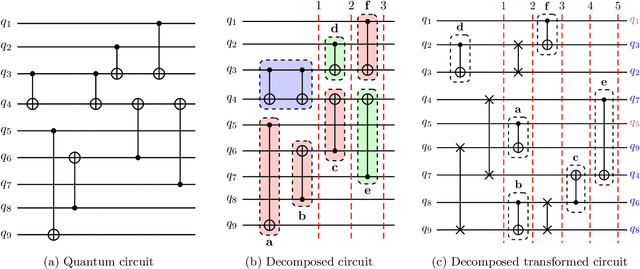
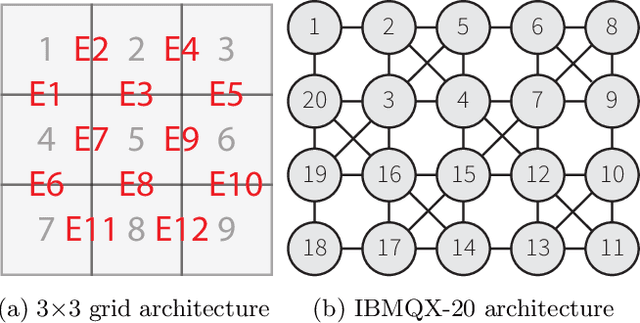
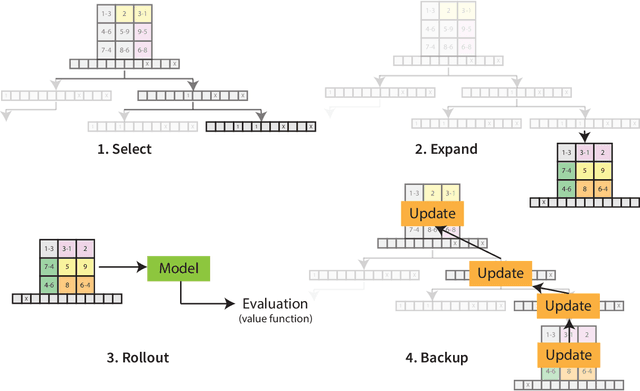
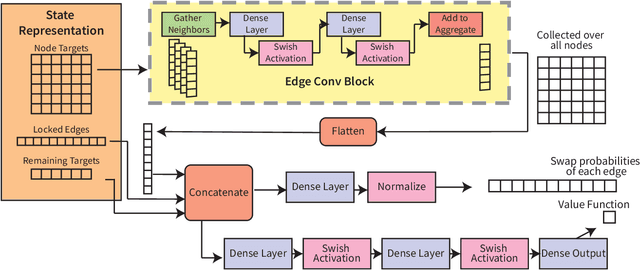
Near-term quantum hardware can support two-qubit operations only on the qubits that can interact with each other. Therefore, to execute an arbitrary quantum circuit on the hardware, compilers have to first perform the task of qubit routing, i.e., to transform the quantum circuit either by inserting additional SWAP gates or by reversing existing CNOT gates to satisfy the connectivity constraints of the target topology. We propose a procedure for qubit routing that is architecture agnostic and that outperforms other available routing implementations on various circuit benchmarks. The depth of the transformed quantum circuits is minimised by utilizing the Monte Carlo tree search to perform qubit routing, aided by a Graph neural network that evaluates the value function and action probabilities for each state.