TopoMap++: A faster and more space efficient technique to compute projections with topological guarantees

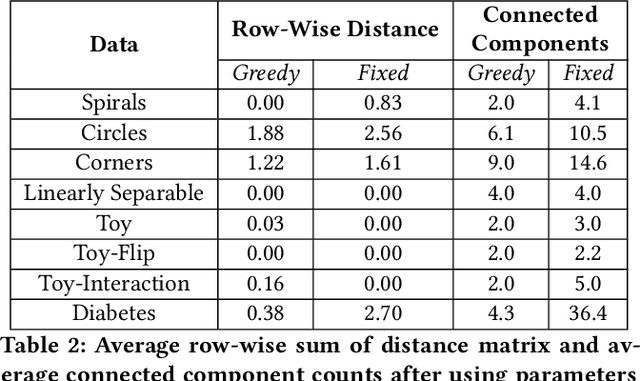
High-dimensional data, characterized by many features, can be difficult to visualize effectively. Dimensionality reduction techniques, such as PCA, UMAP, and t-SNE, address this challenge by projecting the data into a lower-dimensional space while preserving important relationships. TopoMap is another technique that excels at preserving the underlying structure of the data, leading to interpretable visualizations. In particular, TopoMap maps the high-dimensional data into a visual space, guaranteeing that the 0-dimensional persistence diagram of the Rips filtration of the visual space matches the one from the high-dimensional data. However, the original TopoMap algorithm can be slow and its layout can be too sparse for large and complex datasets. In this paper, we propose three improvements to TopoMap: 1) a more space-efficient layout, 2) a significantly faster implementation, and 3) a novel TreeMap-based representation that makes use of the topological hierarchy to aid the exploration of the projections. These advancements make TopoMap, now referred to as TopoMap++, a more powerful tool for visualizing high-dimensional data which we demonstrate through different use case scenarios.

Topological Representations of Local Explanations

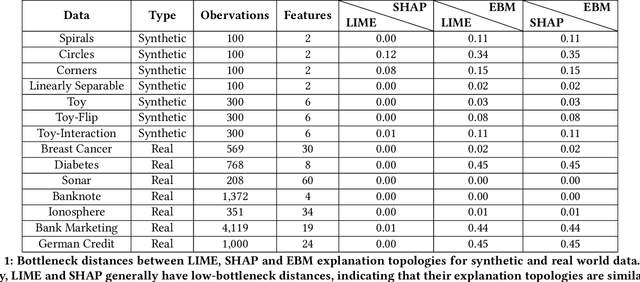
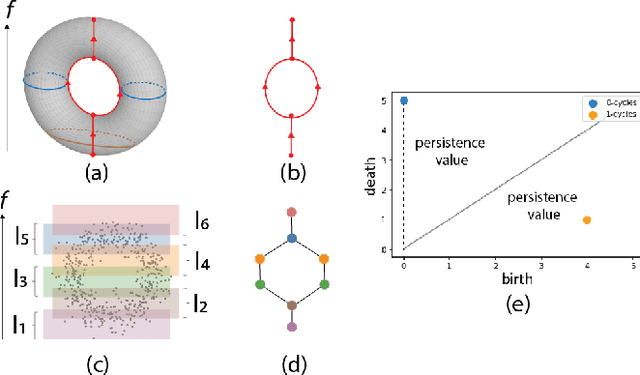
Local explainability methods -- those which seek to generate an explanation for each prediction -- are becoming increasingly prevalent due to the need for practitioners to rationalize their model outputs. However, comparing local explainability methods is difficult since they each generate outputs in various scales and dimensions. Furthermore, due to the stochastic nature of some explainability methods, it is possible for different runs of a method to produce contradictory explanations for a given observation. In this paper, we propose a topology-based framework to extract a simplified representation from a set of local explanations. We do so by first modeling the relationship between the explanation space and the model predictions as a scalar function. Then, we compute the topological skeleton of this function. This topological skeleton acts as a signature for such functions, which we use to compare different explanation methods. We demonstrate that our framework can not only reliably identify differences between explainability techniques but also provides stable representations. Then, we show how our framework can be used to identify appropriate parameters for local explainability methods. Our framework is simple, does not require complex optimizations, and can be broadly applied to most local explanation methods. We believe the practicality and versatility of our approach will help promote topology-based approaches as a tool for understanding and comparing explanation methods.

Valuing Player Actions in Counter-Strike: Global Offensive

Esports, despite its expanding interest, lacks fundamental sports analytics resources such as accessible data or proven and reproducible analytical frameworks. Even Counter-Strike: Global Offensive (CSGO), the second most popular esport, suffers from these problems. Thus, quantitative evaluation of CSGO players, a task important to teams, media, bettors and fans, is difficult. To address this, we introduce (1) a data model for CSGO with an open-source implementation; (2) a graph distance measure for defining distances in CSGO; and (3) a context-aware framework to value players' actions based on changes in their team's chances of winning. Using over 70 million in-game CSGO events, we demonstrate our framework's consistency and independence compared to existing valuation frameworks. We also provide use cases demonstrating high-impact play identification and uncertainty estimation.

TopoMap: A 0-dimensional Homology Preserving Projection of High-Dimensional Data

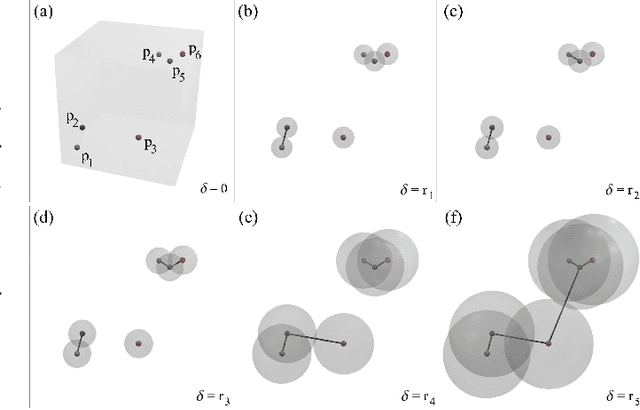
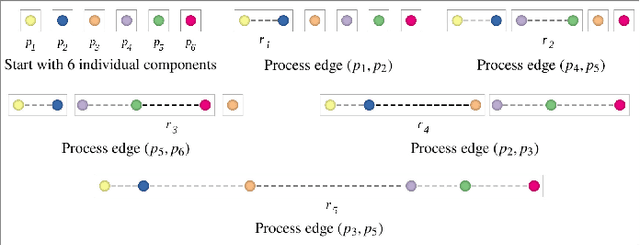
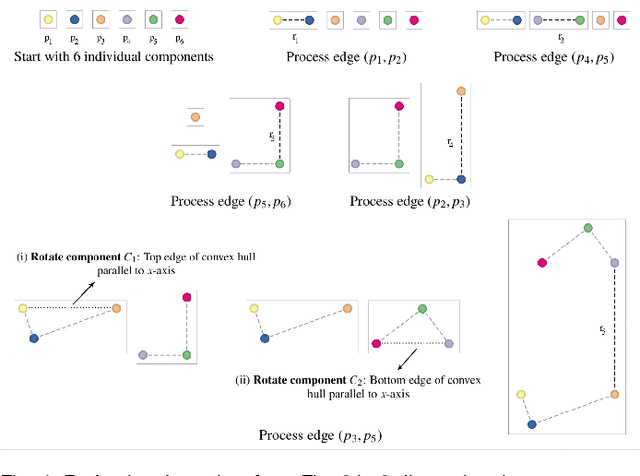
Multidimensional Projection is a fundamental tool for high-dimensional data analytics and visualization. With very few exceptions, projection techniques are designed to map data from a high-dimensional space to a visual space so as to preserve some dissimilarity (similarity) measure, such as the Euclidean distance for example. In fact, although adopting distinct mathematical formulations designed to favor different aspects of the data, most multidimensional projection methods strive to preserve dissimilarity measures that encapsulate geometric properties such as distances or the proximity relation between data objects. However, geometric relations are not the only interesting property to be preserved in a projection. For instance, the analysis of particular structures such as clusters and outliers could be more reliably performed if the mapping process gives some guarantee as to topological invariants such as connected components and loops. This paper introduces TopoMap, a novel projection technique which provides topological guarantees during the mapping process. In particular, the proposed method performs the mapping from a high-dimensional space to a visual space, while preserving the 0-dimensional persistence diagram of the Rips filtration of the high-dimensional data, ensuring that the filtrations generate the same connected components when applied to the original as well as projected data. The presented case studies show that the topological guarantee provided by TopoMap not only brings confidence to the visual analytic process but also can be used to assist in the assessment of other projection methods.