Haige Shen
Stochastic Variational Inference via Upper Bound
Dec 02, 2019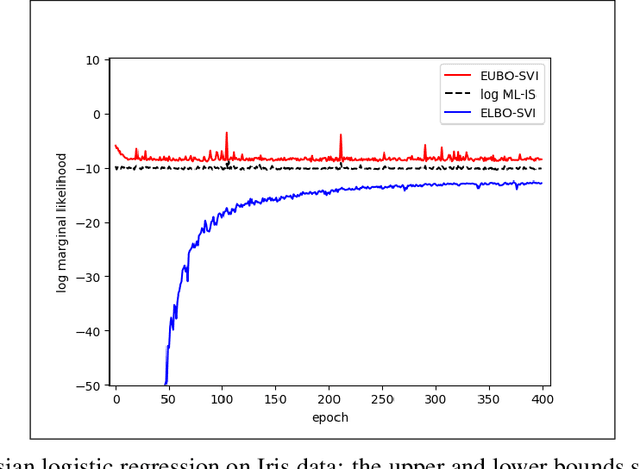
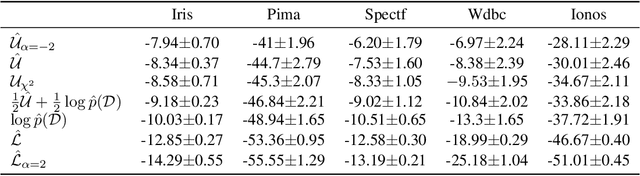
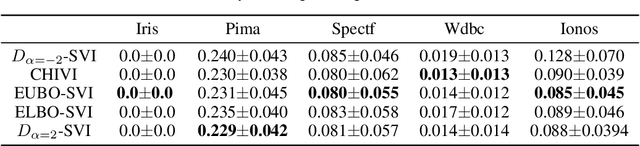
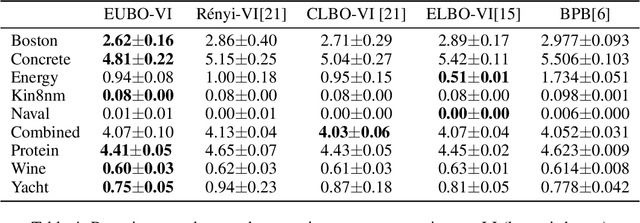
Abstract:Stochastic variational inference (SVI) plays a key role in Bayesian deep learning. Recently various divergences have been proposed to design the surrogate loss for variational inference. We present a simple upper bound of the evidence as the surrogate loss. This evidence upper bound (EUBO) equals to the log marginal likelihood plus the KL-divergence between the posterior and the proposal. We show that the proposed EUBO is tighter than previous upper bounds introduced by $\chi$-divergence or $\alpha$-divergence. To facilitate scalable inference, we present the numerical approximation of the gradient of the EUBO and apply the SGD algorithm to optimize the variational parameters iteratively. Simulation study with Bayesian logistic regression shows that the upper and lower bounds well sandwich the evidence and the proposed upper bound is favorably tight. For Bayesian neural network, the proposed EUBO-VI algorithm outperforms state-of-the-art results for various examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge