A global constraint for the capacitated single-item lot-sizing problem

The goal of this paper is to set a constraint programming framework to solve lot-sizing problems. More specifically, we consider a single-item lot-sizing problem with time-varying lower and upper bounds for production and inventory. The cost structure includes time-varying holding costs, unitary production costs and setup costs. We establish a new lower bound for this problem by using a subtle time decomposition. We formulate this NP-hard problem as a global constraint and show that bound consistency can be achieved in pseudo-polynomial time and when not including the costs, in polynomial time. We develop filtering rules based on existing dynamic programming algorithms, exploiting the above mentioned time decomposition for difficult instances. In a numerical study, we compare several formulations of the problem: mixed integer linear programming, constraint programming and dynamic programming. We show that our global constraint is able to find solutions, unlike the decomposed constraint programming model and that constraint programming can be competitive, in particular when adding combinatorial side constraints.

A Combinatorial Optimisation Approach to Designing Dual-Parented Long-Reach Passive Optical Networks

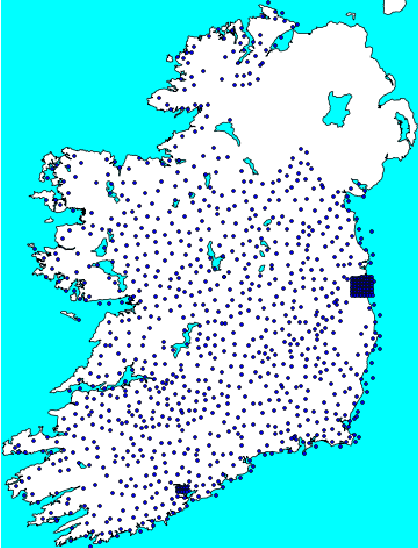
We present an application focused on the design of resilient long-reach passive optical networks. We specifically consider dual-parented networks whereby each customer must be connected to two metro sites via local exchange sites. An important property of such a placement is resilience to single metro node failure. The objective of the application is to determine the optimal position of a set of metro nodes such that the total optical fibre length is minimized. We prove that this problem is NP-Complete. We present two alternative combinatorial optimisation approaches to finding an optimal metro node placement using: a mixed integer linear programming (MIP) formulation of the problem; and, a hybrid approach that uses clustering as a preprocessing step. We consider a detailed case-study based on a network for Ireland. The hybrid approach scales well and finds solutions that are close to optimal, with a runtime that is two orders-of-magnitude better than the MIP model.