An inferential measure of dependence between two systems using Bayesian model comparison

We propose to quantify dependence between two systems $X$ and $Y$ in a dataset $D$ based on the Bayesian comparison of two models: one, $H_0$, of statistical independence and another one, $H_1$, of dependence. In this framework, dependence between $X$ and $Y$ in $D$, denoted $B(X,Y|D)$, is quantified as $P(H_1|D)$, the posterior probability for the model of dependence given $D$, or any strictly increasing function thereof. It is therefore a measure of the evidence for dependence between $X$ and $Y$ as modeled by $H_1$ and observed in $D$. We review several statistical models and reconsider standard results in the light of $B(X,Y|D)$ as a measure of dependence. Using simulations, we focus on two specific issues: the effect of noise and the behavior of $B(X,Y|D)$ when $H_1$ has a parameter coding for the intensity of dependence. We then derive some general properties of $B(X,Y|D)$, showing that it quantifies the information contained in $D$ in favor of $H_1$ versus $H_0$. While some of these properties are typical of what is expected from a valid measure of dependence, others are novel and naturally appear as desired features for specific measures of dependence, which we call inferential. We finally put these results in perspective; in particular, we discuss the consequences of using the Bayesian framework as well as the similarities and differences between $B(X,Y|D)$ and mutual information.

Automated extraction of mutual independence patterns using Bayesian comparison of partition models

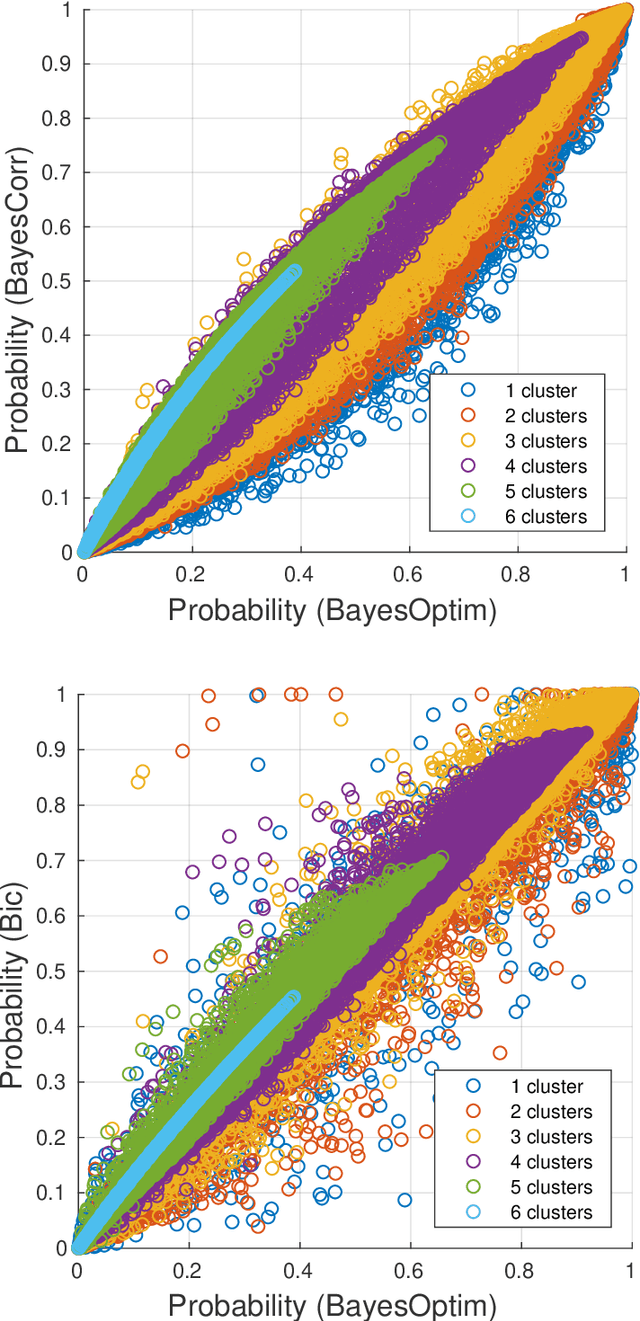
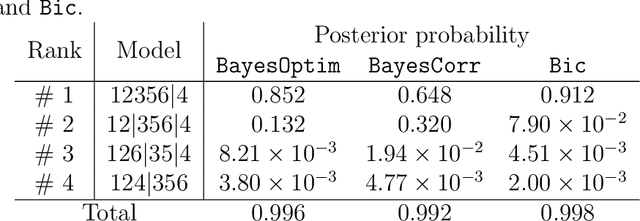
Mutual independence is a key concept in statistics that characterizes the structural relationships between variables. Existing methods to investigate mutual independence rely on the definition of two competing models, one being nested into the other and used to generate a null distribution for a statistic of interest, usually under the asymptotic assumption of large sample size. As such, these methods have a very restricted scope of application. In the present manuscript, we propose to change the investigation of mutual independence from a hypothesis-driven task that can only be applied in very specific cases to a blind and automated search within patterns of mutual independence. To this end, we treat the issue as one of model comparison that we solve in a Bayesian framework. We show the relationship between such an approach and existing methods in the case of multivariate normal distributions as well as cross-classified multinomial distributions. We propose a general Markov chain Monte Carlo (MCMC) algorithm to numerically approximate the posterior distribution on the space of all patterns of mutual independence. The relevance of the method is demonstrated on synthetic data as well as two real datasets, showing the unique insight provided by this approach.

A Bayesian alternative to mutual information for the hierarchical clustering of dependent random variables

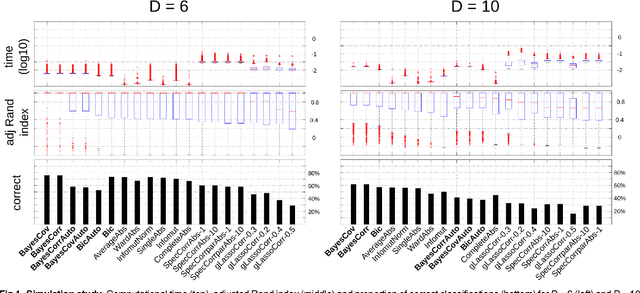
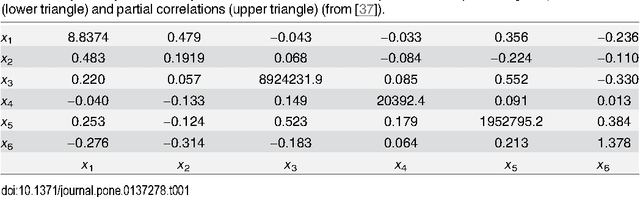
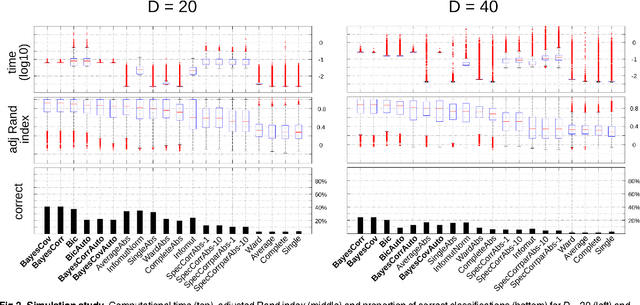
The use of mutual information as a similarity measure in agglomerative hierarchical clustering (AHC) raises an important issue: some correction needs to be applied for the dimensionality of variables. In this work, we formulate the decision of merging dependent multivariate normal variables in an AHC procedure as a Bayesian model comparison. We found that the Bayesian formulation naturally shrinks the empirical covariance matrix towards a matrix set a priori (e.g., the identity), provides an automated stopping rule, and corrects for dimensionality using a term that scales up the measure as a function of the dimensionality of the variables. Also, the resulting log Bayes factor is asymptotically proportional to the plug-in estimate of mutual information, with an additive correction for dimensionality in agreement with the Bayesian information criterion. We investigated the behavior of these Bayesian alternatives (in exact and asymptotic forms) to mutual information on simulated and real data. An encouraging result was first derived on simulations: the hierarchical clustering based on the log Bayes factor outperformed off-the-shelf clustering techniques as well as raw and normalized mutual information in terms of classification accuracy. On a toy example, we found that the Bayesian approaches led to results that were similar to those of mutual information clustering techniques, with the advantage of an automated thresholding. On real functional magnetic resonance imaging (fMRI) datasets measuring brain activity, it identified clusters consistent with the established outcome of standard procedures. On this application, normalized mutual information had a highly atypical behavior, in the sense that it systematically favored very large clusters. These initial experiments suggest that the proposed Bayesian alternatives to mutual information are a useful new tool for hierarchical clustering.