Giovanni C. Santia
Is space a word, too?
Oct 20, 2017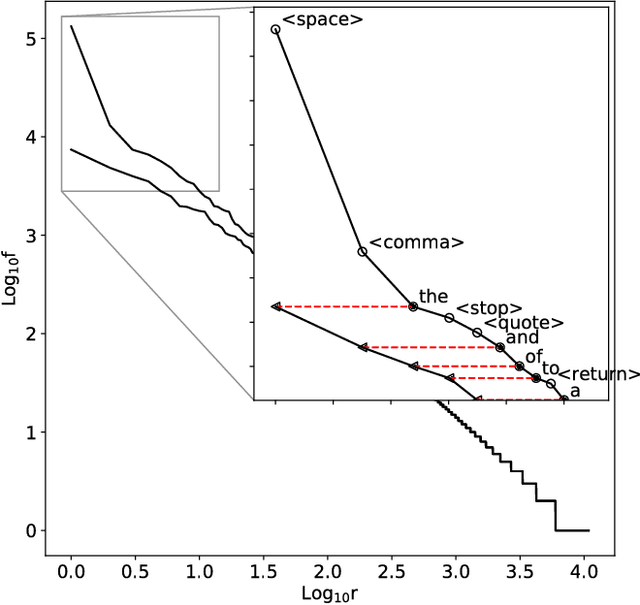
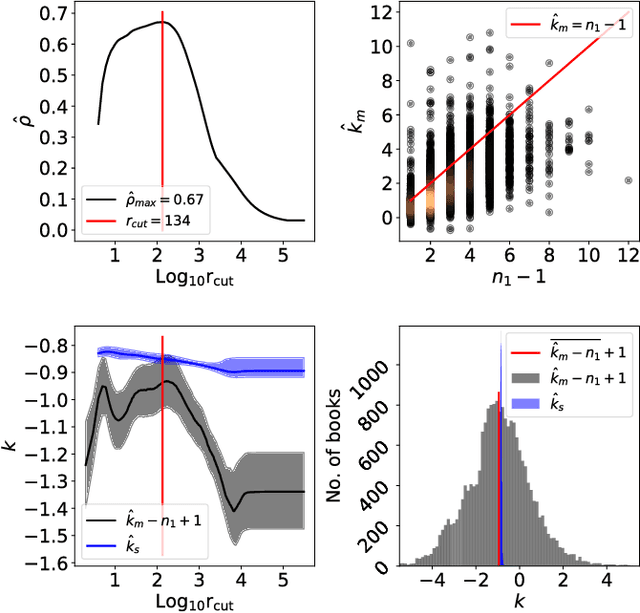
Abstract:For words, rank-frequency distributions have long been heralded for adherence to a potentially-universal phenomenon known as Zipf's law. The hypothetical form of this empirical phenomenon was refined by Ben\^{i}ot Mandelbrot to that which is presently referred to as the Zipf-Mandelbrot law. Parallel to this, Herbet Simon proposed a selection model potentially explaining Zipf's law. However, a significant dispute between Simon and Mandelbrot, notable empirical exceptions, and the lack of a strong empirical connection between Simon's model and the Zipf-Mandelbrot law have left the questions of universality and mechanistic generation open. We offer a resolution to these issues by exhibiting how the dark matter of word segmentation, i.e., space, punctuation, etc., connect the Zipf-Mandelbrot law to Simon's mechanistic process. This explains Mandelbrot's refinement as no more than a fudge factor, accommodating the effects of the exclusion of the rank-frequency dark matter. Thus, integrating these non-word objects resolves a more-generalized rank-frequency law. Since this relies upon the integration of space, etc., we find support for the hypothesis that $all$ are generated by common processes, indicating from a physical perspective that space is a word, too.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge