Compact representations of convolutional neural networks via weight pruning and quantization

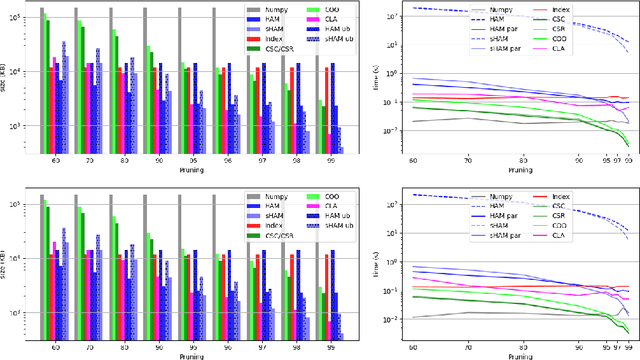
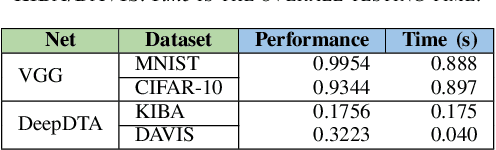
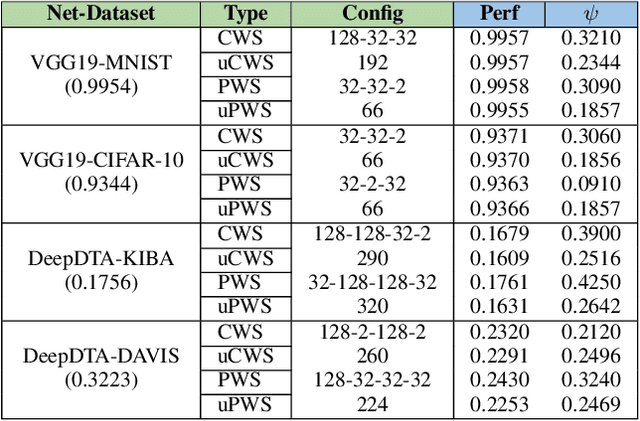
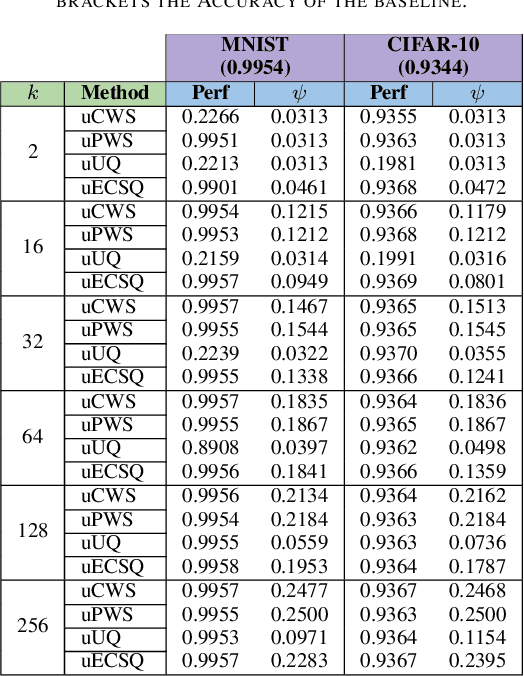
The state-of-the-art performance for several real-world problems is currently reached by convolutional neural networks (CNN). Such learning models exploit recent results in the field of deep learning, typically leading to highly performing, yet very large neural networks with (at least) millions of parameters. As a result, the deployment of such models is not possible when only small amounts of RAM are available, or in general within resource-limited platforms, and strategies to compress CNNs became thus of paramount importance. In this paper we propose a novel lossless storage format for CNNs based on source coding and leveraging both weight pruning and quantization. We theoretically derive the space upper bounds for the proposed structures, showing their relationship with both sparsity and quantization levels of the weight matrices. Both compression rates and excution times have been tested against reference methods for matrix compression, and an empirical evaluation of state-of-the-art quantization schemes based on weight sharing is also discussed, to assess their impact on the performance when applied to both convolutional and fully connected layers. On four benchmarks for classification and regression problems and comparing to the baseline pre-trained uncompressed network, we achieved a reduction of space occupancy up to 0.6% on fully connected layers and 5.44% on the whole network, while performing at least as competitive as the baseline.

Compression strategies and space-conscious representations for deep neural networks

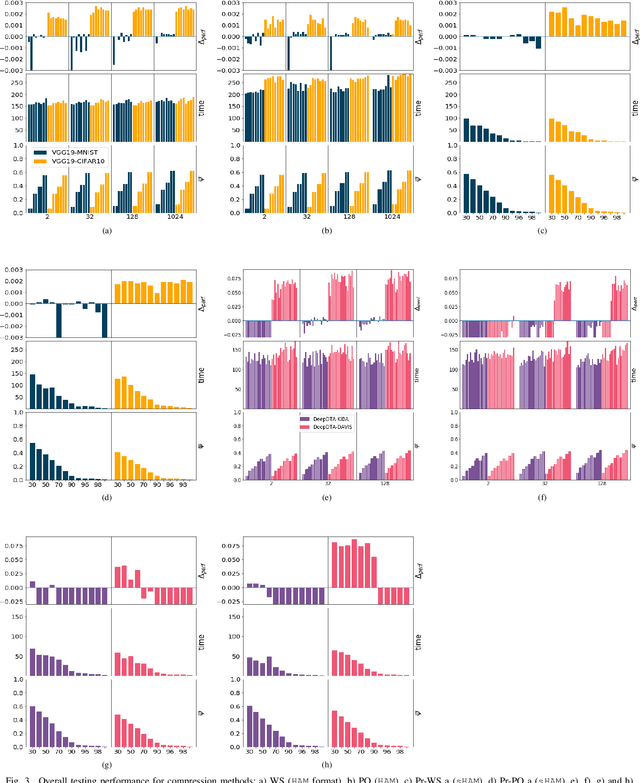
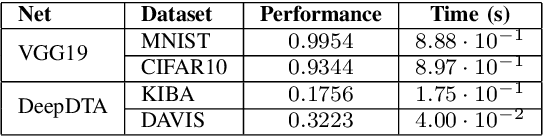
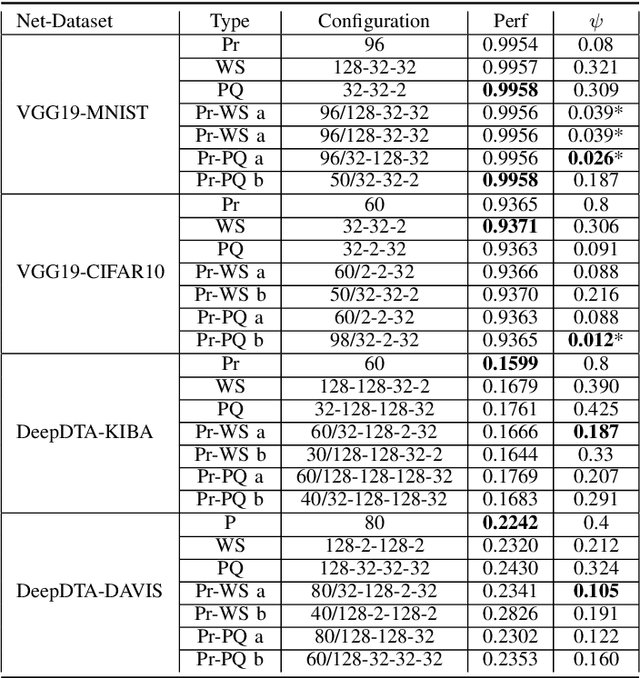
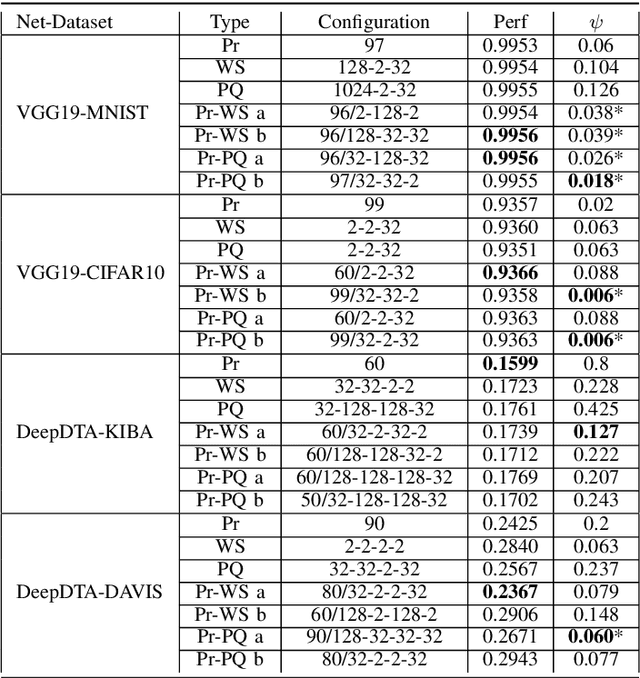
Recent advances in deep learning have made available large, powerful convolutional neural networks (CNN) with state-of-the-art performance in several real-world applications. Unfortunately, these large-sized models have millions of parameters, thus they are not deployable on resource-limited platforms (e.g. where RAM is limited). Compression of CNNs thereby becomes a critical problem to achieve memory-efficient and possibly computationally faster model representations. In this paper, we investigate the impact of lossy compression of CNNs by weight pruning and quantization, and lossless weight matrix representations based on source coding. We tested several combinations of these techniques on four benchmark datasets for classification and regression problems, achieving compression rates up to $165$ times, while preserving or improving the model performance.