Additive Bayesian Network Modelling with the R Package abn

The R package abn is designed to fit additive Bayesian models to observational datasets. It contains routines to score Bayesian networks based on Bayesian or information theoretic formulations of generalized linear models. It is equipped with exact search and greedy search algorithms to select the best network. It supports a possible blend of continuous, discrete and count data and input of prior knowledge at a structural level. The Bayesian implementation supports random effects to control for one-layer clustering. In this paper, we give an overview of the methodology and illustrate the package's functionalities using a veterinary dataset about respiratory diseases in commercial swine production.

Is a single unique Bayesian network enough to accurately represent your data?

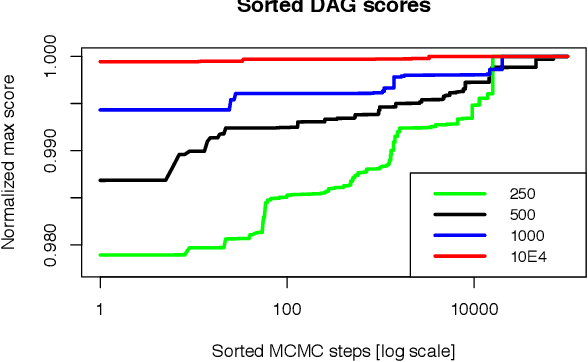
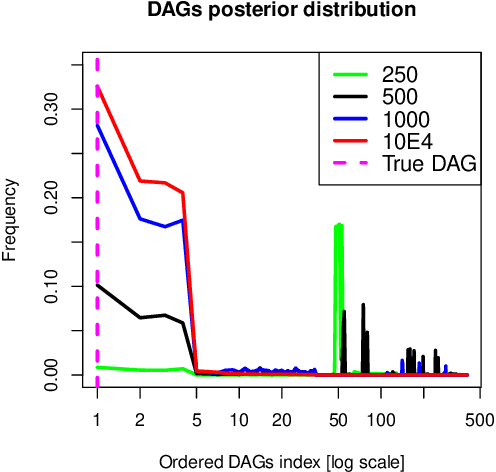
Bayesian network (BN) modelling is extensively used in systems epidemiology. Usually it consists in selecting and reporting the best-fitting structure conditional to the data. A major practical concern is avoiding overfitting, on account of its extreme flexibility and its modelling richness. Many approaches have been proposed to control for overfitting. Unfortunately, they essentially all rely on very crude decisions that result in too simplistic approaches for such complex systems. In practice, with limited data sampled from complex system, this approach seems too simplistic. An alternative would be to use the Monte Carlo Markov chain model choice (MC3) over the network to learn the landscape of reasonably supported networks, and then to present all possible arcs with their MCMC support. This paper presents an R implementation, called mcmcabn, of a flexible structural MC3 that is accessible to non-specialists.

Comparison between Suitable Priors for Additive Bayesian Networks

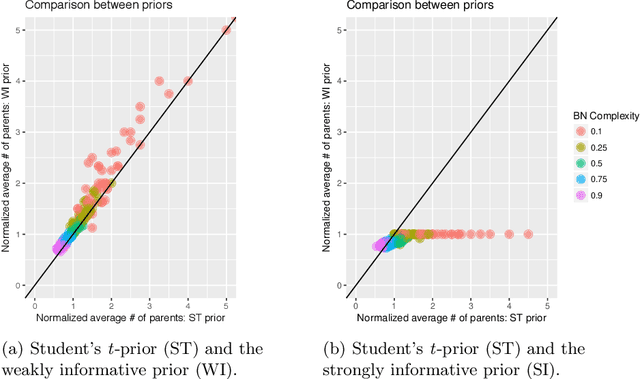
Additive Bayesian networks are types of graphical models that extend the usual Bayesian generalized linear model to multiple dependent variables through the factorisation of the joint probability distribution of the underlying variables. When fitting an ABN model, the choice of the prior of the parameters is of crucial importance. If an inadequate prior - like a too weakly informative one - is used, data separation and data sparsity lead to issues in the model selection process. In this work a simulation study between two weakly and a strongly informative priors is presented. As weakly informative prior we use a zero mean Gaussian prior with a large variance, currently implemented in the R-package abn. The second prior belongs to the Student's t-distribution, specifically designed for logistic regressions and, finally, the strongly informative prior is again Gaussian with mean equal to true parameter value and a small variance. We compare the impact of these priors on the accuracy of the learned additive Bayesian network in function of different parameters. We create a simulation study to illustrate Lindley's paradox based on the prior choice. We then conclude by highlighting the good performance of the informative Student's t-prior and the limited impact of the Lindley's paradox. Finally, suggestions for further developments are provided.

Information-Theoretic Scoring Rules to Learn Additive Bayesian Network Applied to Epidemiology

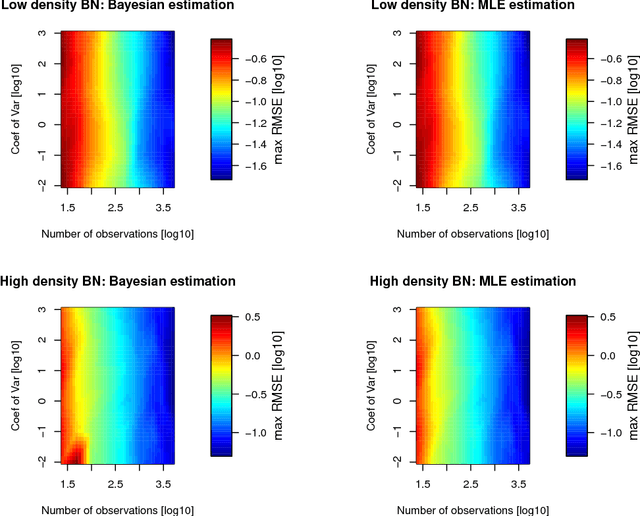
Bayesian network modelling is a well adapted approach to study messy and highly correlated datasets which are very common in, e.g., systems epidemiology. A popular approach to learn a Bayesian network from an observational datasets is to identify the maximum a posteriori network in a search-and-score approach. Many scores have been proposed both Bayesian or frequentist based. In an applied perspective, a suitable approach would allow multiple distributions for the data and is robust enough to run autonomously. A promising framework to compute scores are generalized linear models. Indeed, there exists fast algorithms for estimation and many tailored solutions to common epidemiological issues. The purpose of this paper is to present an R package abn that has an implementation of multiple frequentist scores and some realistic simulations that show its usability and performance. It includes features to deal efficiently with data separation and adjustment which are very common in systems epidemiology.

varrank: an R package for variable ranking based on mutual information with applications to observed systemic datasets

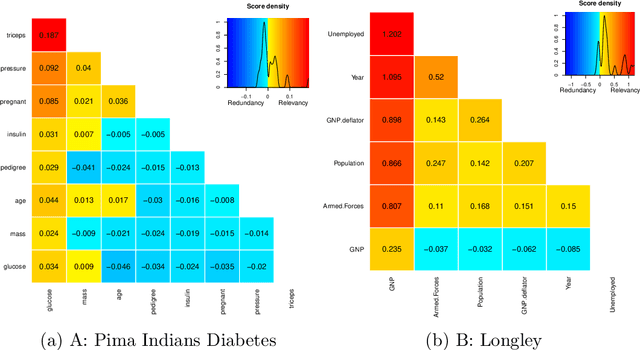
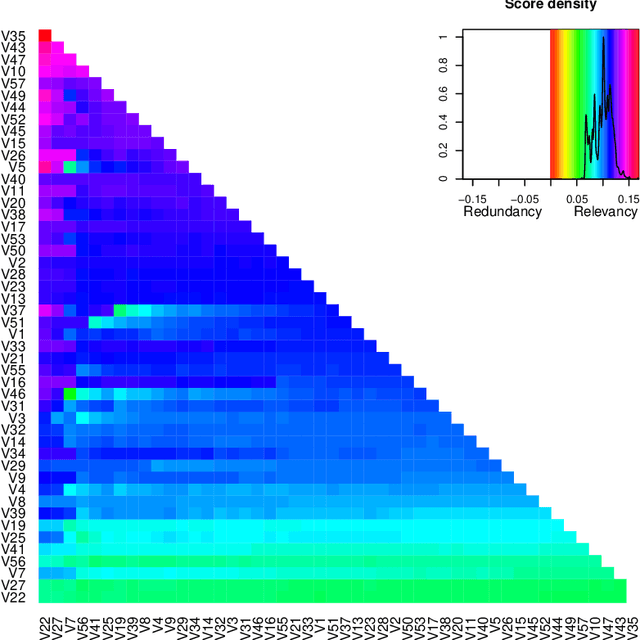
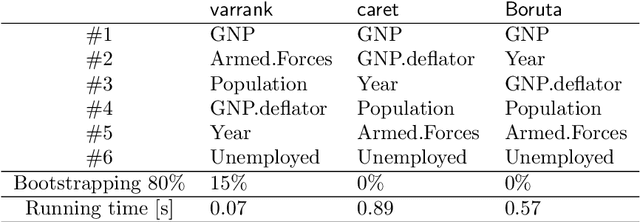
This article describes the R package varrank. It has a flexible implementation of heuristic approaches which perform variable ranking based on mutual information. The package is particularly suitable for exploring multivariate datasets requiring a holistic analysis. The core functionality is a general implementation of the minimum redundancy maximum relevance (mRMRe) model. This approach is based on information theory metrics. It is compatible with discrete and continuous data which are discretised using a large choice of possible rules. The two main problems that can be addressed by this package are the selection of the most representative variables for modeling a collection of variables of interest, i.e., dimension reduction, and variable ranking with respect to a set of variables of interest.