Cyclic Supports in Recursive Bipolar Argumentation Frameworks: Semantics and LP Mapping

Dung's Abstract Argumentation Framework (AF) has emerged as a key formalism for argumentation in Artificial Intelligence. It has been extended in several directions, including the possibility to express supports, leading to the development of the Bipolar Argumentation Framework (BAF), and recursive attacks and supports, resulting in the Recursive BAF (Rec-BAF). Different interpretations of supports have been proposed, whereas for Rec-BAF (where the target of attacks and supports may also be attacks and supports) even different semantics for attacks have been defined. However, the semantics of these frameworks have either not been defined in the presence of support cycles, or are often quite intricate in terms of the involved definitions. We encompass this limitation and present classical semantics for general BAF and Rec-BAF and show that the semantics for specific BAF and Rec-BAF frameworks can be defined by very simple and intuitive modifications of that defined for the case of AF. This is achieved by providing a modular definition of the sets of defeated and acceptable elements for each AF-based framework. We also characterize, in an elegant and uniform way, the semantics of general BAF and Rec-BAF in terms of logic programming and partial stable model semantics.

Counterfactual and Semifactual Explanations in Abstract Argumentation: Formal Foundations, Complexity and Computation

Explainable Artificial Intelligence and Formal Argumentation have received significant attention in recent years. Argumentation-based systems often lack explainability while supporting decision-making processes. Counterfactual and semifactual explanations are interpretability techniques that provide insights into the outcome of a model by generating alternative hypothetical instances. While there has been important work on counterfactual and semifactual explanations for Machine Learning models, less attention has been devoted to these kinds of problems in argumentation. In this paper, we explore counterfactual and semifactual reasoning in abstract Argumentation Framework. We investigate the computational complexity of counterfactual- and semifactual-based reasoning problems, showing that they are generally harder than classical argumentation problems such as credulous and skeptical acceptance. Finally, we show that counterfactual and semifactual queries can be encoded in weak-constrained Argumentation Framework, and provide a computational strategy through ASP solvers.

Even-if Explanations: Formal Foundations, Priorities and Complexity

EXplainable AI has received significant attention in recent years. Machine learning models often operate as black boxes, lacking explainability and transparency while supporting decision-making processes. Local post-hoc explainability queries attempt to answer why individual inputs are classified in a certain way by a given model. While there has been important work on counterfactual explanations, less attention has been devoted to semifactual ones. In this paper, we focus on local post-hoc explainability queries within the semifactual `even-if' thinking and their computational complexity among different classes of models, and show that both linear and tree-based models are strictly more interpretable than neural networks. After this, we introduce a preference-based framework that enables users to personalize explanations based on their preferences, both in the case of semifactuals and counterfactuals, enhancing interpretability and user-centricity. Finally, we explore the complexity of several interpretability problems in the proposed preference-based framework and provide algorithms for polynomial cases.

On the Semantics of Abstract Argumentation Frameworks: A Logic Programming Approach

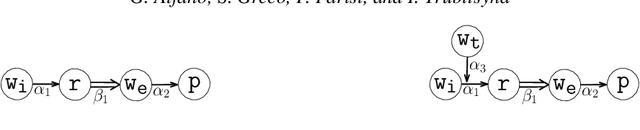
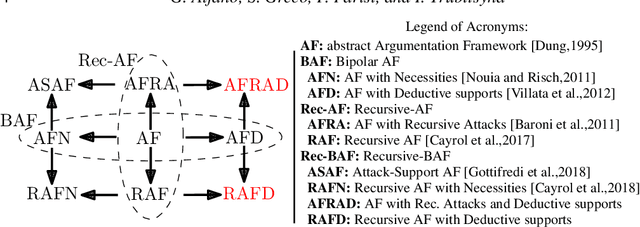
Recently there has been an increasing interest in frameworks extending Dung's abstract Argumentation Framework (AF). Popular extensions include bipolar AFs and AFs with recursive attacks and necessary supports. Although the relationships between AF semantics and Partial Stable Models (PSMs) of logic programs has been deeply investigated, this is not the case for more general frameworks extending AF. In this paper we explore the relationships between AF-based frameworks and PSMs. We show that every AF-based framework $\Delta$ can be translated into a logic program $P_\Delta$ so that the extensions prescribed by different semantics of $\Delta$ coincide with subsets of the PSMs of $P_\Delta$. We provide a logic programming approach that characterizes, in an elegant and uniform way, the semantics of several AF-based frameworks. This result allows also to define the semantics for new AF-based frameworks, such as AFs with recursive attacks and recursive deductive supports. Under consideration for publication in Theory and Practice of Logic Programming.