Approximating Optimal Labelings for Temporal Connectivity

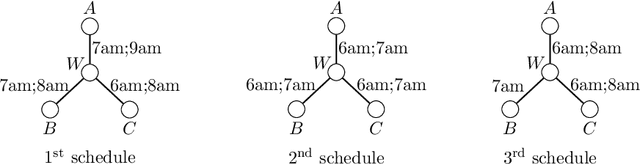
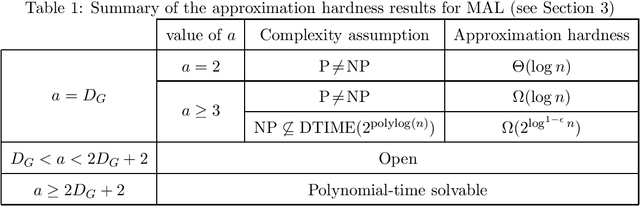
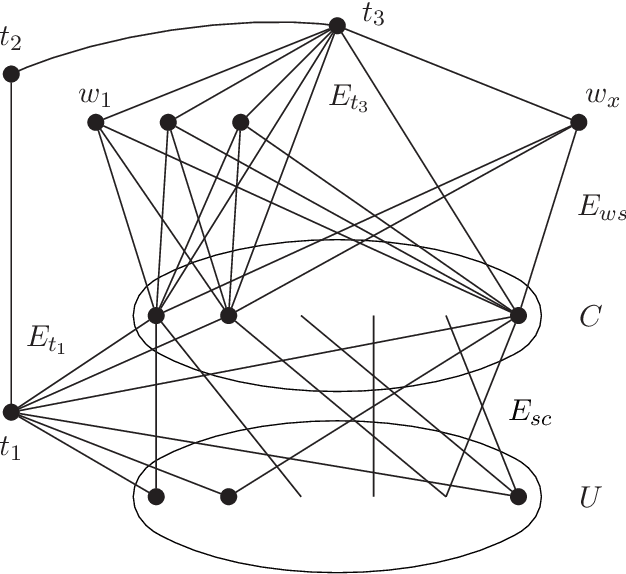
In a temporal graph the edge set dynamically changes over time according to a set of time-labels associated with each edge that indicates at which time-steps the edge is available. Two vertices are connected if there is a path connecting them in which the edges are traversed in increasing order of their labels. We study the problem of scheduling the availability time of the edges of a temporal graph in such a way that all pairs of vertices are connected within a given maximum allowed time $a$ and the overall number of labels is minimized. The problem, known as \emph{Minimum Aged Labeling} (MAL), has several applications in logistics, distribution scheduling, and information spreading in social networks, where carefully choosing the time-labels can significantly reduce infrastructure costs, fuel consumption, or greenhouse gases. The problem MAL has previously been proved to be NP-complete on undirected graphs and \APX-hard on directed graphs. In this paper, we extend our knowledge on the complexity and approximability of MAL in several directions. We first show that the problem cannot be approximated within a factor better than $O(\log n)$ when $a\geq 2$, unless $\text{P} = \text{NP}$, and a factor better than $2^{\log ^{1-\epsilon} n}$ when $a\geq 3$, unless $\text{NP}\subseteq \text{DTIME}(2^{\text{polylog}(n)})$, where $n$ is the number of vertices in the graph. Then we give a set of approximation algorithms that, under some conditions, almost match these lower bounds. In particular, we show that the approximation depends on a relation between $a$ and the diameter of the input graph. We further establish a connection with a foundational optimization problem on static graphs called \emph{Diameter Constrained Spanning Subgraph} (DCSS) and show that our hardness results also apply to DCSS.

Computation and Bribery of Voting Power in Delegative Simple Games

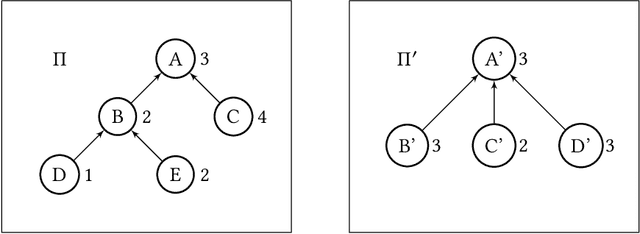
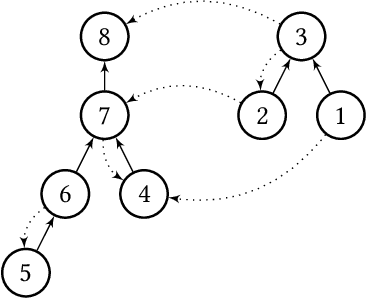
Weighted voting games is one of the most important classes of cooperative games. Recently, Zhang and Grossi [53] proposed a variant of this class, called delegative simple games, which is well suited to analyse the relative importance of each voter in liquid democracy elections. Moreover, they defined a power index, called the delagative Banzhaf index to compute the importance of each agent (i.e., both voters and delegators) in a delegation graph based on two key parameters: the total voting weight she has accumulated and the structure of supports she receives from her delegators. We obtain several results related to delegative simple games. We first propose a pseudo-polynomial time algorithm to compute the delegative Banzhaf and Shapley-Shubik values in delegative simple games. We then investigate a bribery problem where the goal is to maximize/minimize the voting power/weight of a given voter in a delegation graph by changing at most a fixed number of delegations. We show that the problems of minimizing/maximizing a voter's power index value are strongly NP-hard. Furthermore, we prove that having a better approximation guarantee than $1-1/e$ to maximize the voting weight of a voter is not possible, unless $P = NP$, then we provide some parameterized complexity results for this problem. Finally, we show that finding a delegation graph with a given number of gurus that maximizes the minimum power index value an agent can have is a computationally hard problem.

When Can Liquid Democracy Unveil the Truth?

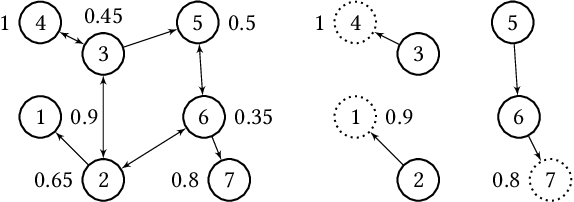
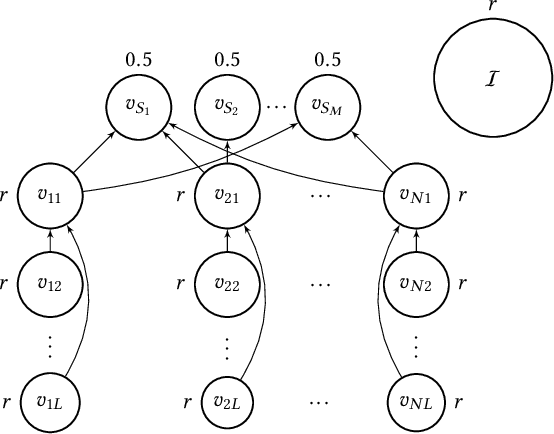
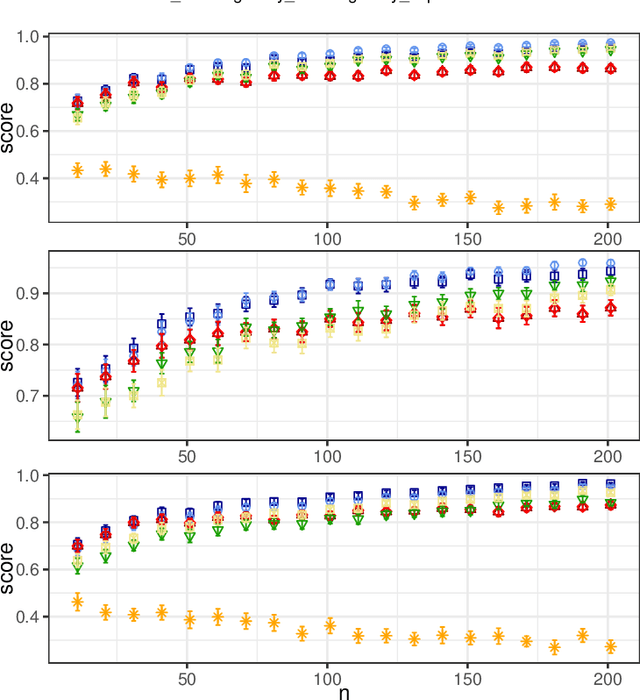
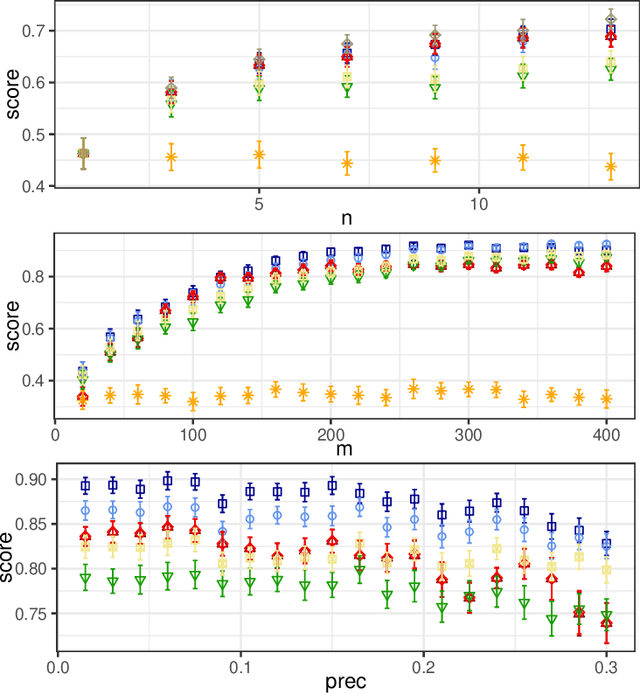
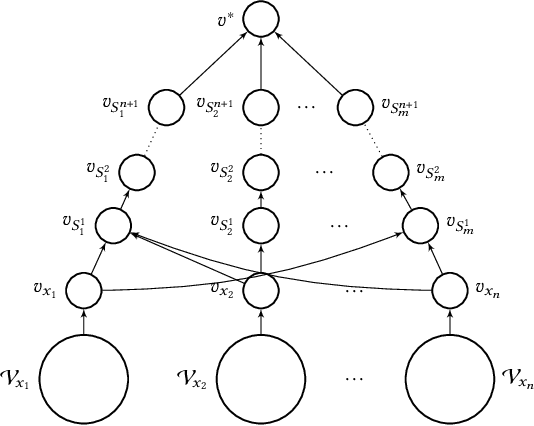
In this paper, we investigate the so-called ODP-problem that has been formulated by Caragiannis and Micha [10]. Here, we are in a setting with two election alternatives out of which one is assumed to be correct. In ODP, the goal is to organise the delegations in the social network in order to maximize the probability that the correct alternative, referred to as ground truth, is elected. While the problem is known to be computationally hard, we strengthen existing hardness results by providing a novel strong approximation hardness result: For any positive constant $C$, we prove that, unless $P=NP$, there is no polynomial-time algorithm for ODP that achieves an approximation guarantee of $\alpha \ge (\ln n)^{-C}$, where $n$ is the number of voters. The reduction designed for this result uses poorly connected social networks in which some voters suffer from misinformation. Interestingly, under some hypothesis on either the accuracies of voters or the connectivity of the network, we obtain a polynomial-time $1/2$-approximation algorithm. This observation proves formally that the connectivity of the social network is a key feature for the efficiency of the liquid democracy paradigm. Lastly, we run extensive simulations and observe that simple algorithms (working either in a centralized or decentralized way) outperform direct democracy on a large class of instances. Overall, our contributions yield new insights on the question in which situations liquid democracy can be beneficial.

Better Bounds on the Adaptivity Gap of Influence Maximization under Full-adoption Feedback

In the influence maximization (IM) problem, we are given a social network and a budget $k$, and we look for a set of $k$ nodes in the network, called seeds, that maximize the expected number of nodes that are reached by an influence cascade generated by the seeds, according to some stochastic model for influence diffusion. In this paper, we study the adaptive IM, where the nodes are selected sequentially one by one, and the decision on the $i$th seed can be based on the observed cascade produced by the first $i-1$ seeds. We focus on the full-adoption feedback in which we can observe the entire cascade of each previously selected seed and on the independent cascade model where each edge is associated with an independent probability of diffusing influence. Our main result is the first sub-linear upper bound that holds for any graph. Specifically, we show that the adaptivity gap is upper-bounded by $\lceil n^{1/3}\rceil $, where $n$ is the number of nodes in the graph. Moreover, we improve over the known upper bound for in-arborescences from $\frac{2e}{e-1}\approx 3.16$ to $\frac{2e^2}{e^2-1}\approx 2.31$. Finally, we study $\alpha$-bounded graphs, a class of undirected graphs in which the sum of node degrees higher than two is at most $\alpha$, and show that the adaptivity gap is upper-bounded by $\sqrt{\alpha}+O(1)$. Moreover, we show that in 0-bounded graphs, i.e. undirected graphs in which each connected component is a path or a cycle, the adaptivity gap is at most $\frac{3e^3}{e^3-1}\approx 3.16$. To prove our bounds, we introduce new techniques to relate adaptive policies with non-adaptive ones that might be of their own interest.